Ej67. Se quiere saber cuál es la duración media de unas zapatillas. Lo que ocurre es que si se lo preguntamos al zapatero, él no la conoce.
Pero en cambio, sabe la probabilidad de que duren menos de 3 meses antes de romperse es de 0.1. ¿Cuál es la duración media?
Realizamos una recopilación de datos que nos ofrece el problema:
· X ≡ 'Tiempo de las zapatillas antes de romperse'.
· La variable X se distribuye de forma exponencial: X ~ exp(β) meses.
Lo único que sabemos es lo siguiente:
· P(X <3) = 0.1
Para obtener la solución a este problema nos apoyaremos en la función de distribución acumulada desde -∞ hasta x, en nuestro caso, al tratarse de una distribución exponencial su función de densidad es la que se muestra a continuación:
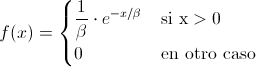
Por lo tanto, ya tenemos el índice inferior de la integral para obtener la función de distribución acumulada, sera desde 0 hasta x, el límite superior emplearemos el dato que nos ofrece el enunciado:
· x = 2
Ya disponemos de los límites de integración, desde 0 hasta 2. Por lo tanto, debemos integrar la función de densidad de la distribución exponencial entre esos límites:
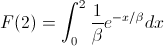
La solución de la integral es sencilla, con un cambio de variable:
· y = -x/β
· dy = -(1/β)dx
Sustituimos:
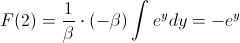
Deshacemos el cambio de variable:
· y = -x/β
Aplicamos los límites de integración, la solución de la integral es:
Pues bien, simplemente aplicamos el dato del enunciado:
· F(2) = P(X ≤ 2) = 0.1
Por lo tanto:
· F(2) = 1 - e(-2/β) = 0.1
Despejamos:
· e(-2/β) = 0.9
Para resolver dicha igualdad, aplicamos logaritmo neperiano en ambas partes:
Despejamos el parámetro que nos interesa β:
· β = -2/Ln(0.9) ≈ 18.982443
Sabiendo que la esperanza matemática de la distribución exponencial es el propio parámetro medio, obtenemos la solución al primer apartado:
· μ = E[X] = β = 18.982443
Es decir, se esperan que dichas zapatillas duren casi 19 meses.
· NOTA: Este ejercicio se ha obtenido de los comentarios del capítulo: Variables Aleatorias Continuas.





0 comentarios:
Publicar un comentario