No todas las variables aleatorias son discretas, este capítulo tratará sobre el segundo tipo general de variables aleatorias, llamadas variables aleatorias continuas.
Se dice que una variable aleatoria, por ejemplo X, es continua si los conjuntos de valores posibles es un intervalo completo de números, es decir, si para alguna A
Función de Densidad de Probabilidad.
También llamada: Distribución de Probabilidad, sea X una variable aleatoria continua, entonces una función de densidad de probabilidad de X es una función f(x) tal que para dos números cualesquiera a y b.
La probabilidad de que X tome un valor en el intervalo [a, b] es el área arriba de este intervalo y bajo la gráfica de una función de densidad. La curva f(x) se llama curva de densidad.
Para que f(x) sea una función de densidad de probabilidad, se deben satisfacer las siguientes condiciones:
2.
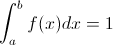
Proposición: Si X es una variable aleatoria continua, entonces para cualquier valor de c, P( X = c) = 0. En definitiva, la probabilidad asignada a algún valor en particular es cero, mientras que la probabilidad de un intervalo no depende de si está incluido en cualquiera de sus puntos terminales.
Función de Distribución Acumulada.
La función de distribución acumulada, F(x), para una variable aleatoria continua X, está definida para todo número x mediante:
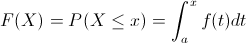
Para cada x, F(x) es el área bajo la curva de densidad a la izquierda de x. F(x) se incrementará de manera uniforme cuando aumenta x.
La función de distribución acumulada es muy útil para calcular probabilidades: Sea X una variable aleatoria continua con función de densidad de probabilidad f(x) y función de distribución acumulada F(x). Entonces, para cualquier número a, la probabilidad es:
Y para dos números cualesquiera a y b, con b > a
Relación entre la Función de Probabilidad de Densidad y la Función de Distribución Acumulada.
Si X es una variable aleatoria continua con función de distribución de probabilidad f(x) y función de distribución acumulada F(x), entonces:
Esperanza de una Variable Aleatoria Continua.
La esperanza, promedio, valor esperado o media de una variable aleatoria continua X con función de densidad de probabilidad f(x) es:
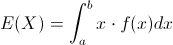
A veces, se desea calcular la esperanza de alguna función h(X) de la variable aleatoria X, si se considera h(X) como una nueva variable aleatoria Y, su esperanza es:
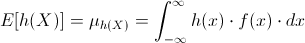
Siempre que
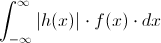
Sea finita.
Varianza de una Variable Aleatoria Continua.
La varianza de una variable aleatoria continua X con función de densidad de probabilidad f(x) es:
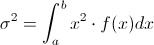
La raíz cuadrada positiva, σ, de la varianza de X, se denomina: desviación típica de X.
Proposiciones de Esperanza y Varianza de una Variable Aleatoria Continua.
Sea X una variable aleatoria continua y sean a y b dos números reales cualesquiera, se verifica que:
1. E(a·X + b) = a·E(X) + b
2. Var(a·X + b) = a²·Var(X)
3. Var(X) = E(X²) - [E(X)]²
Distribución Uniforme.
Se dice que una variable aleatoria continua X, que toma todos los valores del intervalo [a, b] real, sigue una distribución uniforme de parámetros a y b, si su función de densidad de probabilidad es:
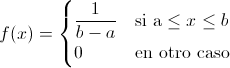
Se representa por: X ~ U(a, b).
Su función de distribución acumulada, F(x) es:
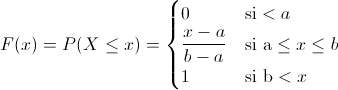
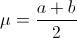
Y la varianza de la distribución uniforme viene expresada por:
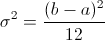
Distribución Normal.
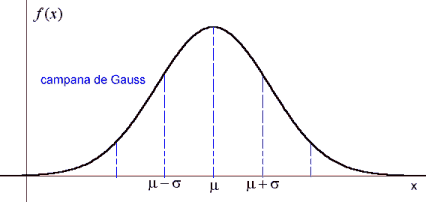
Se dice que una variable aleatoria continua X, tiene una distribución normal o de Gauss de parámetros μ y σ, si su función de densidad de probabilidad es:
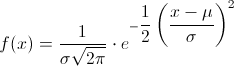
Se representa la distribución normal, por: X ~ N(μ, σ).
La media de la distribución normal viene dada por:
Y la varianza de la distribución normal viene expresada por:
La representación gráfica así cómo los significados de la esperanza y varianza son:
Distribución Normal No Estándar (Tipicación).
Si X tiene una distribución normal con media μ y desviación estándar σ, entonces:
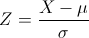
Se dice que tiene una distribución normal estándar.
Aproximación de la Distribución Binomial por la Normal.
Sea X una variable aleatoria continua que sigue una distribución de probabilidad binomial: X ~ B(n, p), si n·p ≥ 5 y por ende, n·q ≥ 5, se pude aproximar por una distribución normal:
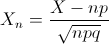
La media, al igual que en la distribución binomial, viene dada por:
Y la varianza, al igual que en la distribución binomial, viene expresada por:
Corrección por continuidad:
1. P(a ≤ X ≤ b) = P(a - 0.5 ≤ X ≤ b + 0.5)
2. P(a <.X ≤ b) = P(a + 0.5 ≤ X ≤ b + 0.5)
3. P(a ≤ X <.b) = P(a - 0.5 ≤ X ≤ b - 0.5)
4. P(a < X <.b) = P(a + 0.5 ≤ X ≤ b - 0.5)
Aproximación de la Distribución de Poisson por la Normal.
Sea X una variable aleatoria continua que sigue una distribución de probabilidad de Poisson: X ~ P(λ), si λ > 25, se pude aproximar por una distribución normal:
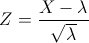
Por lo tanto, sigue N(0,1) de forma aproximada.
La media, al igual que en la distribución de Poisson, viene dada por:
Y la varianza, al igual que en la distribución de Poisson, viene expresada por:
Corrección por continuidad:
1. P(a ≤ X ≤ b) = P(a - 0.5 ≤ X ≤ b + 0.5)
2. P(a <.X ≤ b) = P(a + 0.5 ≤ X ≤ b + 0.5)
3. P(a ≤ X <.b) = P(a - 0.5 ≤ X ≤ b - 0.5)
4. P(a <.X <.b) = P(a + 0.5 ≤ X ≤ b - 0.5)
Distribución Exponencial.
Se dice que una variable aleatoria continua X, tiene una distribución exponencial de parámetro β, si su función de densidad de probabilidad es:
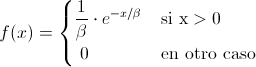
Para β > 0.
Se representa por: X ~ Exp(β).
La media de la distribución normal viene dada por:
Y la varianza de la distribución normal viene expresada por:
La distribución exponencial posee una característica a tener en cuenta: Carencia de memoria.
Sea X ~ Exp(β). Si x, y ∈ Z⁺, se verifica que:
A continuación, se disponen de una colección de problemas resueltos.





105 comentarios:
Hola primeramente felicitarte por el blog.
Tengo una duda; Si me dicen P(x<3)=0.1, como puedo hallar la esperanza?
Se supone que tengo que me tienen que dar la funcion para obtener E(x)... pero solo me dan ese dato.
Te agradeceria si me puedieses ayudar.
Un saludo desde BCN
Buenas:
Creo que que simplemente con ese dato, el ejercicio es más bien teórico, es decir, explicar cómo obtendrías la esperanza dependiendo del carácter de la variable aleatoria X.
¿Y por qué te digo esto? Pues porque no se especifica si la variable aleatoria X sea discreta o continua, dependiendo de que tipo sea la esperanza matemática se calculará de una forma u otra.
· Si X es una Variable Aleatoria Discreta
En el caso de no pertenecer a ninguna distribución conocida: Binomial, Poisson, Geométrica, etc, se debe tener los sucesos de x y su correspondiente probabilidad, es decir, crear un tabla cómo la que sigue:
x.........0....1......2....3.....n
P(x)...0.1..0.2..0.4..0.1...a
Incluso puede que no esté definidas todas las probabilidades, por lo que con notas como:
· P(X < 3) = 0.1
· ΣP(X) = 1
Se podría montar un sistemas de ecuaciones y obtener las probabilidades de los sucesos que faltan para posteriormente, obtener la esperanza matemática mediante su expresión:
· E[X] = Σx·P(x)
En caso de que la variable aleatoria discreta pertenezca a alguna de las distribuciones conocidas, aplicaremos la esperanza de cada distribución.
· Si X es una Variable Aleatoria Continua
En el caso de no pertenecer a ninguna distribución conocida: Normal, Uniforme, Exponencial, etc, se debe tener la función de densidad de probabilidad o la función de distribución acumulada para posteriormente, aplicar la expresión matemática de la esperanza.
No es necesario que te den la función tal cual, pero el enunciado debe definir que patrón seguir y el intervalo válido de trabajo.
En caso de que la variable aleatoria continua pertenezca a alguna de las distribuciones conocidas, aplicaremos la esperanza de cada distribución.
· NOTA: Para la distribución de Cauchy, la esperanza no existe.
Gracias por tu comentario y si tienes la solución no se te olvide de exponerla.
Hola Manuel.
A ver me han dado una pista.
Me han dicho que se trata de una distribución exponencial.
Te pongo el ejercicio para que lo veas:
Nosotros queremos saber cuál es la duración media de unas zapatillas. Lo que ocurre es que se lo
preguntamos al zapatero y no lo sabe, pero sabe la probabilidad de que duren menos de 3 meses antes de romperse que es de 0,1.
a) ¿Cuál es la duración media?
b) Calcula la probabilidad de que dure más de 6 meses.
c) Representa las probabilidades de los apartados anteriores.
Mi hipotesis seria:
Utilizar la función de densidad de la exponencial, con un sumatorio de las integrales de (aquí dudo) [0,3] cambiando x por 0,1 y 2.
Y todo esto igual a 0.1 y despejar beta que seria E(x).
Como lo ves?
Muchas gracias por contestar, y nuevamente enhorabuena me está ayudando muchísimo
Buenas:
Con el enunciado, no hace falta que te den ninguna pista, ya que se deduce que la probabilidad es al primer fallo/acierto, por lo tanto estamos antes una distribución exponencial (aunque las pistas de vez en cuando nunca vienen mal).
Los pasos que mencionan para obtener la esperanza son más o menos acertados, no hace falta hacer ningún sumatorio ya que estamos trabajando con variables aleatorias continuas.
El procedimiento a seguir es el siguiente:
· Obtener la función de distribución acumulada con los datos dados. Lo único que sabemos es:
· P(X < 3) = 0.1
Ese dato equivale a la función de distribución acumulada al siguiente:
· F(2) = P(X ≤ 2)
Y sabemos que la función de distribución acumulada es la integral desde -∞ hasta x, en nuestro caso, al tratarse de una distribución exponencial nos condiciona a:
· x > 0
· Será cero en otro caso.
Por lo tanto, ya tenemos el índice inferior de la integral para obtener la función de distribución acumulada, sera desde 0 hasta x, el límite superior emplearemos el dato que nos ofrece el enunciado:
· x = 2
Ya disponemos de los límites de integración, desde 0 hasta 2. Por lo tanto, debemos integrar la función de densidad de la distribución exponencial entre esos límites:
· F(2) = P(X ≤ 2) = ʃ(1/β)·e^(-x/β)dx
· NOTA: Los límites de la integral sería desde 0 hasta 2, por comentarios no me permite ponerlo bien.
La solución de la integral es sencilla, con un cambio de variable:
· y = -x/β
· dy = -(1/β)dx
Sustituimos:
ʃ(1/β)·e^(-x/β)dx = (1/β)·(-β)·ʃe^(y)dy = -ʃe^(y)dy
La integral es inmediata y deshacemos el cambio de variable:
· ʃe^(y)dy = e^(y)
· y = -x/β
Aplicamos los límites de integración, la solución de la integral es:
· F(2) = P(X ≤ 2) = ʃ(1/β)·e^(-x/β)dx = -e^(-x/β)|0-2 = -[e^(-2/β) - e^0] = -[e^(-2/β) - 1] = 1 - e^(-2/β)
Pues bien, simplemente aplicamos el dato del enunciado:
· F(2) = P(X ≤ 2) = 0.1
Por lo tanto:
· F(2) = 1 - e^(-2/β) = 0.1
Despejamos:
e^(-2/β) = 0.9
Para resolver dicha igualdad, aplicamos logaritmo neperiano en ambas partes:
-2/β = Ln(0.9)
Despejamos el parámetro que nos interesa β:
· β = -2/Ln(0.9) ≈ 18.982443
Sabiendo que la esperanza matemática de la distribución exponencial es el propio parámetro medio, obtenemos la solución al primer apartado:
· μ = E[X] = β = 18.982443
Es decir, se esperan que dichas zapatillas duren casi 19 meses.
Los demás apartados te los dejo para ti, ya teniendo el parámetro medio es pan comido.
· PD: Para comprobar los resultados puedes emplear software estadístico, por ejemplo en R:
> qexp(0.1, rate=1/18.982443, lower.tail = T)
[1] 2
Vemos que 2 es el espacio que nos dan en el enunciado del problema: F(2) = P(X ≤ 2) = 0.1
Un saludo y gracias por tu comentario.
Grandioso, Enorme!!!
Muchas grácias no hiba mal encaminado... (si no fuese por lo del sumatório)
Muchos de los de mi clase de la universidad, estamos encantados con tu blog.
A mi me está ayudando muchisimo.
Continua con este trabajo, por que de verdad es magnífico.
Saludos desde BCN
Hola Manuel! tienes un blog q no he encontrado por ninguna parte.
Mis felicitaciones y respeto.
Gracias.
apesar de q tenemos un buen prof, Me ha ayudado bastante en entender mejor los problemas!
Buenas Nélida:
Me alegro mucho de que te hayan servido de ayuda los contenidos que exponemos en el blog.
Gracias por tu comentario y un saludo.
Hola,
me gustaría saber cómo pasa de:
"· P(X < 3) = 0.1
Ese dato equivale a la función de distribución acumulada al siguiente:
· F(2) = P(X ≤ 2)"
Es decir, como cálcula que la probabilidad de que duren menos de 3 meses es 0.1, equivale a "F(2) = P(X ≤ 2)".
Muchas gracias de antemano por su ayuda.
Buenas:
La pregunta es sencilla, cuando decimos que una variable aleatoria tiene un rango menor que tres:
· P(X < 3)
Es lo mismo decir, que dicha variable aleatoria tiene un rango menor o igual a dos:
· P(X ≤ 2)
Es decir, al ser menor que tres obligamos a la variable a comprender los números desde menos infinito hasta dos.
Y si nos vamos a la teoría, la definición de la Distribución Acumulada no es más que la siguiente:
· F(X) = P(X ≤ x)
Un saludo y gracias por tu comentario.
Buenos días,
¿me podría ayudar con el siguiente ejercicio?
"sea X una variable aleatoria con función de densidad:
2x si x pertenece [0,1]
0, si x no pertenece [0,1]
Se pide:
- hallar la función de distribución de Y=min(X, 0.75).
- Calcular P{Y>0.25}
Muchas gracias por su ayuda
Buenas:
La función de distribución acumulada de la variable aleatoria continua X es:
· Si X < 0:.........F(x) = 0
· Si 0 ≤ X ≤ 1:....F(x) = x²
· Si X > 1:.........F(X) = 1
La forma de obtenerla es fácil, como ejemplo están los problemas comprendidos desde el 1 hasta el 10 de este capitulo.
Ahora bien, ¿qué significa Y = min(X, 0.75)?
¿Se refiere al mínimo valor que toma la variable aleatoria X?
Si es así, el resultado sería: Y pertenece (0, 0.75), y su función de distribución acumulada sería:
· Si Y ≤ 0:..............F(y) = 0
· Si 0 < Y < 0.75:....F(y) = y²
· Si Y ≥ 0.75:.........F(y) = 1
Y la probabilidad a obtener sería:
P(Y > 0.25) = 1 - P(Y ≤ 0.25) = 1 - 0.25² = 0.9375.
Quedo a la espera de que me corrijas o des más información del problema. Un saludo y gracias por tu comentario.
Sí justo se refiere al mínimo valor que toma X. Muchas gracias ahora lo tengo claro. Sin embargo tengo una nueva duda (espero no abusar), si en lugar de darme la función de densidad, me dicen que X tiene una distribución uniforme en [0,1] y que halle la función de distribución de Y = min(X, 0.75) ¿cómo lo haría?.
Si me dan la función de densidad y gracias a su explicación y ejercicios, ahora ya tengo claro como hallar la función de distribución. Pero si sólo me dicen que la variable es uniforme ¿como lo hago?. Es decir, si te dan un modelo (uniforme, exponencial, normal...) como hallas la función de distribución?
Gracias de nuevo por todo,
Buenas:
En caso de que te den una función conocida: Uniforme, Exponencial, etc. Los pasos a seguir son exactamente iguales que si te dieran una función cualquiera.
Eso sí, para las distribuciones conocidas deberán darte su función de densidad o , como suele ser habitual, te la tendrás que aprender de memoria por ser bastante habituales y comunes de usar.
Una vez tengas la función de densidad, la integras tal como dice la definición y teoría para obtener la función acumulada.
Más arriba en los comentarios, alguien planteó un problema con una función exponencial, si lo observas, verás que para obtener la solución tuve que, previamente, calcular la función acumulada tal y como indica su definición.
En los problemas también tienes ejercicios con dichas funciones conocidas y cómo se obtienen sus funciones acumuladas.
Otra manera, aunque no te la recomiendo, es que te aprendas de memoria ambas funciones: Densidad y Acumulada. Aunque repito, no te lo recomiendo.
Y con respecto a cómo se emplearía en el problema la distribución uniforme, pues es fácil, los límites serías desde 0 hasta 0.75. Una vez tenido los límites ya puedes integrar la función de densidad de la uniforme para obtener la acumulada.
Un saludo y gracias por tu comentario.
Buenos días,
tiene usted algo publicado de funciones de densidad de dos variables? es decir, hallar la función de densidad conjunta de dos variables por ejemplo x e y?
Gracias.
Buenas:
En estos momentos no está disponible, es un apartado al igual que el de estudios de contrastes no paramétricos que tenemos en mente publicar.
Pero como muy pronto, empezaríamos en Marzo del año que viene.
Lo siento, un saludo y gracias por tu comentario.
Buenas noches,
¿me puede ayudar en este ejercicio?
"Sea X una variable aleatoria con función de densidad uniforme en (-1,1). Calcular la función de densidad de la variable Y=X^2".
Mi libro, primero halla la función de distribución y para ello, toma como límites de integración lo siguiente:
{Y≤y}={X^2≤y}={-√y ≤ X ≤√y}
Con los límites de -√ y +√ halla la integral de 1/2, y le da como resultado √y.
Mi duda es dado, que si X toma valores entre (-1,1), Y tomará valores entre (0,1), ¿por tanto los límites de integración no debían ser 0 y √y?
Espero haberme explicado..
Muchas gracias de antemano y un saludo
Buenas:
Voy a resolver el ejercicio a ver si me entero de tu duda.
· X ~ U(-1, 1). Distribución Uniforme.
Su función de densidad es:
· f(x) = 1/2, -1 ≤ x ≤ 1 (0 en otro caso)
Bien, nos piden obtener la función de densidad de la variable Y, la cual se expresa de la siguiente forma:
· Y = X²
No es más que un cambio de variable, pero en fin, para obtener su función de densidad vamos previamente a obtener, su función de distribución acumulada. Para tal fin, aplicamos la definición:
· F(Y) = P(Y ≤ y)
Realizamos el cambio de variable:
· F(Y) = P(Y ≤ y) = P(X² ≤ y) = P(-√y ≤ x ≤ √y)
Pues bien, sabemos que f(x) = 1/2, realizamos la integral desde -√y hasta √y para obtener la función de distribución acumulada:
· F(Y) = P(Y ≤ y) = ʃ(1/2)dx = -(1/2)x|√y--(-√y) = (1/2)·[√y + √y] = √y
· NOTA: Los límites de la integral sería desde -√y hasta √y, por comentarios no me permite ponerlo bien.
Pues bien, ya tenemos la función de distribución acumulada de Y:
· F(Y) = √y
Cuyo intervalo de acción es de 0 ≤ y ≤ 1 (No puede ir desde -1 hasta 1 ya que la raíz cuadrada de un número negativo no es válida).
Pues bien, simplemente nos queda deshacer el camino recorrido para obtener la función de densidad:
· f(y) = F'(Y) = [y¹/²]' = (2√y)⁻¹
Ya está resuelto el problema, como ves los propios pasos que debes seguir te dictan las propias claves del problema.
Los límites de integración de Y no deben ser 0 y √y porque la integral que se realiza es de la variable X,
Un saludo y gracias por tu comentario.
Gracias, lo tengo claro, sin embargo, mirando más ejercicios veo que si en lugar de que X tenga función de densidad uniforme en (-1,1), la tiene en (0,1), los límites de integración sí son (0,√), cuando según este ejercicio sería (y realizando el mismo cambio de variable):
F(Y) = P(Y ≤ y) = P(X² ≤ y) = P(-√y ≤ x ≤ √y).
En mi libro de texto si X es (0,1), se integra en (0,√y) y no en
(-√y, √y).
Gracias de nuevo.
Buenas:
Vamos a ver, no es lo mismo que la variable aleatoria continua esté definida en un rango u otro.
Si está en el intervalo (-1, 1) pues se tendrá en cuenta los límites de integración desde negativo hasta positivo.
Pero en cambio, si la misma variable aleatoria continua está en el intervalo (0, 1), sólo se tendrá en cuenta desde 0 hasta positivo.
Esto es así ya que para valores distintos de los que marca el rango de la función de densidad, su valor es cero.
A ver un ejemplo, sea X una variable aleatoria continua definida en el rango (0, 5).
Para obtener la función de distribución acumulada, no puedo integrar desde, por ejemplo, -5 hasta 5, por la simple razón de que la propia variable sólo está definida desde 0 hasta 5 y por ende, para otros valores su resultado es cero.
Es por ello que sólo integraré desde valores dentro del rango de acción de la función de densidad.
Un saludo.
Aclarado. Ninguna duda!!
Muchas gracias por su ayuda.
Hola Manuel,
No se ven algunas operaciones.
Grácias y un saludo
Buenas:
Si, tenemos un problema grande encima (aunque por fortuna existe solución). Dadme dos días de cómo obtener la mejor forma de solucionarlo y en una semana, estará todo establecido de nuevo.
Perdonar las molestias, un saludo.
ayudenme si tengo 50x^-3/6 de limites de 2 a 10 como integro esto.. ayuda por favor...
Buenas:
La integral es simple e inmediata, es potencia de la variable x, se resuelve de tal manera:
50·ʃx⁻³/⁶dx = 50·(-3/6+1)⁻¹·x⁰´⁵
Aplicamos los límites de integración: [2, 10]:
50/0.5 · [10⁰´⁵ - 2⁰´⁵] ≈ 174.806410
Un saludo.
saludos pero para que sea una funcion d eprobabilidad de densidad tienes que cumplir que f(x)=1
Buenas Mariluz:
Efectivamente, para que una función sea de probabilidad de densidad debe ser positiva y la integral de todo el rango debe valer uno, tal y cómo está explicado en el apartado de teoría (esto es por convenio de que una probabilidad debe ser positiva y menor que la unidad).
En cambio, si te refieres a al comentario de resolver la integral, no determina nada de función de probabilidad ni nada relacionado con la estadística.
Simplemente que se resuelva la integral de la función dada en el intervalo indicado.
Un saludo y gracias por tu comentario.
Hola Manuel!!
Si en un ejercicio me dan la media como puedo obtener los máximos y mínimos (a y b)de la uniforme??
grácias!
Buenas:
Supongo que te darán también el valor de la varianza y así, tendrás dos ecuaciones (μ y σ) con dos incógnitas (a y b).
Si te dan simplemente la media, tendrías una ecuación con dos incógnitas.
Un saludo y gracias por tu comentario.
¡¡Hola!!
Tu blog me está sirviendo de gran ayuda para estudiar.Me sería de gran ayuda si me pudiese resolver el siguiente problema:
La fracción de varones en una población es de 0,58 .Si se extrae al azar una muestra de 100 personas ,¿ Cual es la probabilidad de que el numero de varones de esa muestra esté comprendido entre 50 y 70?.
Muchas Gracias.
Buenas:
Realizamos una recopilación de datos que nos ofrece el enunciado:
· Sea la variable aleatoria X, número de varones.
· Tamaño de la muestra: N = 100 individuos.
· La variable aleatoria discreta X sigue una distribución binomial: X ~ B(100, 0.58)
Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir las siguientes condiciones:
1. n·p ≥ 5 → 100·0.58 = 58 ≥ 5 OK.
2. n·q ≥ 5 → 100·(1-0.58) = 42 ≥ 5 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal.
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(58, √24.36).
La probabilidad que debemos obtener es la siguiente:
· P(50 ≤ X ≤ 70)
Aplicamos el corrector por continuidad y tipificamos:
· P(49.5 ≤ X ≤ 70.5) = P((49.5-58)/√24.36 ≤ Z ≤ (70.5-58)/√24.36) ≈ P(-1.72 ≤ Z ≤ 2.53)
Operamos:
· P(-1.72 ≤ Z ≤ 2.53) = (0.5 + Φ(2.53)) - [1 - (0.5 + Φ(1.72))]
Despejamos y buscamos en la tabla de la Normal:
· P(50 ≤ X ≤ 70) = P(-1.72 ≤ Z ≤ 2.53) = Φ(2.53) + Φ(1.72) = 0.4943 + 0.4573 = 0.9516
Por lo tanto, la probabilidad de que el número de varones esté comprendido entre 50 y 70 de una muestra aleatoria de 100 personas es de 0.9516.
Me alegro que te sea de ayuda el material que exponemos en el blog. Gracias por tu comentario.
Hola Manual, primero que nada me parece genial el aporte que haces, me a ayudado montones...
mi pregunta es:como encuentro la esperanza de una variable aleatoria continua que tiene distinta funcion de densidad para dos intervalo de valores
muchas gracias
Buenas:
Si te fijas en la definición de obtención de la esperanza de una función expuesta en este capítulo, verás que está definida entre el interválo a y b.
Pues para una función de densidad que esté definida en más de un intervalo, se aplica la misma fórmula pero para cada intervalo emplearemos la definición de la función de densidad en ese intervalo concreto y sumamos.
Un saludo y gracias por tu comentario.
eso pensé, pero al hacerlo me da una varianza negativa. Haber si me ayudas
f(x)=-1/3para -1<x<0 y f(x)=-1/3+x para 0<x<2. me piden calcular la varianza
muchas gracias
Buenas:
Si te vas al apartado de Función de Densidad de Probabilidad, verás que para que consideremos una función de estas características se deben satisfacer dos condiciones, la primera es:
1. f(x) > 0,...para todo x.
Esto quiere decir que cualquier función podrá ser considerada como función de densidad de probabilidad si es positiva para cualquier valor de x.
La función que tu me has puesto no cumple con esta condición, excepto en el siguiente intervalo:
· f(x) = -1/3 + x para 1/3 < x < 2
Un saludo.
Hola me gusto mucho el blog y quisiera ver si me puedes ayudar con este ejercicio:
Encontrar la probabilidad de que ninguna de tras lamparas de un semaforo tengan que cambiarse durante kas orimeras 1200 hras de operacion, si el tiempo de vida X de una lampara es una variable aleatoria que tiene la densidad de manera que X se mide en multiplos de 1000 horas.
f(x)={4[0.25-(x-1.5)^3] cuando1<x<2
{0 en otras partes
Buenas:
¿El intervalo está bien definido? o ¿falta algún tipo de información?.
Te digo esto porque según comentas en el enunciado, la variable aleatoria X se mide en múltiplos de 1000 horas, pero el intervalo sólo es de 1 a 2 horas.
Estaría fuera del intervalo de la distribución de probabilidad y por ende, su valor es cero calcules lo que calcules.
Un saludo por tu comentario y revisa el enunciado.
el intervalo esta bien definido yo tome como me pedia a 1200 horas como 1.2 pero no se por que 1 seria 1000 y 2 2000, pero no se como realizarlo bien
Encontrar la probabilidad de que ninguna de tres lamparas de un semaforo tengan que cambiarse durante las primeras 1200 hras de operacion, si el tiempo de vida X de una lampara es una variable aleatoria que tiene la densidad de manera que X se mide en multiplos de 1000 horas.
f(x)={4[0.25-(x-1.5)^3] cuando1<x<2
{0 en otras partes
Buenas:
Lo primero que tienes que hacer es obtener la función acumulada, se calcula a partir de la función de probabilidad, te pongo el resultado directamente (calcularlo no es difícil, es una integral sencilla):
- Para el intervalo: x ≤ 1
· F(x) = 0
- Para el intervalo: 1 < x < 2
· F(x) = -x⁴ + 6x³ - 13.5x² + 14.5x - 6
- Para el intervalo: x ≥ 2
· F(x) = 1
Una vez que tenemos la Función Acumulada del tiempo de vida de una lámpara, vamos a obtener la probabilidad para una lámpara:
· P(X > 1.2) = 1 - P(X ≤ 1.2) = 1 - F(1.2)
Empleamos la expresión matemática de la Función Acumulada acorde a dónde esté el parámetro 1.2, en este caso:
· F(1.2) = -1.2⁴ + 6·1.2³ - 13.5·1.2² + 14.5·1.2 - 6 = 0.2544
Por lo tanto, la probabilidad de que una lámpara (de un semáforo) no tenga que cambiarse durante las 1200 horas primeras es:
· P(X > 1.2) = 1 - F(1.2) = 1 - 0.2544 = 0.7456
Bueno, hasta aquí hemos obtenido la probabilidad de que una lámpara no se cambie durante 1200 horas primeras de operación, pero el enunciado no dicen tres lámparas.
· ¿Las lámparas están conectadas en paralelo o en serie?
· ¿Son independientes entre sí? Supongo que sí.
· ¿Son iguales las lámparas?
En fin, suponemos que las tres son independientes, iguales y que están en serie montadas, por lo tanto, debemos obtener que las tres lámparas no fallen, si denotamos:
· A ≡ 'No falle primera lámpara durante 1200 horas'.
· B ≡ 'No falle segunda lámpara durante 1200 horas'.
· C ≡ 'No falle tercera lámpara durante 1200 horas'.
La probabilidad de no fallar durante 1200 horas es: 0.7456.
Por lo tanto, la probabilidad que nos piden es la siguiente:
· P(A∩B∩C) = P(A)·P(B)·P(C) = 0.7456³ ≈ 0.414493
Un saludo y disculpa el retraso.
ola manuel.me podrías ayudar ,brindandome un ejemplo de Distribuciones y funciones de probabilidad para variables aleatorias Discretas.
Buenas:
Si te vas al menú de la izquierda, en el apartado: Las Riberas Matemáticas, encontrarás en primer lugar, el enlace que pone Estadística dónde están entre otros temas el de Distribuciones y Funciones de Variable Aleatorias Discretas.
· PD: Hola es con H.
Un saludo y gracias por tu comentario.
hola me puedes ayudar? tengo este ejercicio y la verdad no he podido con el.
un profesor ha calculado que el tiempo invertido por los estudiantes en hacer unos ejercicios sigue una distribución normal con media de 150 minutos y una desviación típica de 40 minutos
A-cuantos minutos tarda un alumno si el 90% de sus compañeros tarda mas que el?
Buenas:
Ejercicios muy parecidos al que expones tienes en los ejemplos de este capítulo.
Te lo voy a resolver, definimos el suceso:
· X ≡ 'Tiempo invertido por los estudiantes en hacer unos ejercicios'.
Dicha variable aleatoria sigue una distribución Normal de parámetros:
· X ~ N(150, 40) minutos.
En este problema nos dan los datos de la probabilidad y debemos hallar el valor de la media de la variable aleatoria X que lo satisfaga, tenemos:
· P(X > x) = 1-P(X ≤ x) = 0.9
Operamos:
· P(X ≤ x) = 1-0.9 = 0.1
Tipificamos:
· P(X ≤ x) = P(Z ≤ [x-150]/40) = 0.5+Φ(z) = 0.1
Por lo tanto:
· Φ(z) = 0.1-0.5 = -0.4
Buscamos en las tablas de la Normal y en este caso, no encontramos el valor exacto para 0.4, podemos realizar una interpolación lineal pero en este caso, para simplificar, se escogerá el valor más cercano:
· Z = -1.28
Ya tenemos todos los datos necesarios para resolver este problema:
· (x-150)/40 ≥ -1.28
Despejamos el parámetro que nos interesa:
· x ≥ -(1.28·40)+150 = 98.8
Por lo tanto, un alumno tardará 98.8 minutos en realizar dichos ejercicios si el 90% de sus compañeros tardan más que él.
Un saludo y gracias por tu comentario.
Hola Manuel!
Muy bueno el blog, me esta siendo muy útil para preparar mis exámenes.
Tengo un ejercicio que no sé como resolver.. quizás me puedas orientar un poco:
Sea X una variable aleatoria con funcion de densidad dada por:
f(x)= (3/2)x² ; si -1<=x<=1
0 ; en caso contrario
Hallar la funcion de densidad de
Y = 3-X.
Gracias!
Lorena
Buenas Lorena:
Este tipo de ejercicios es de cambio de variable (normalmente, se suelen enseñar tres tipos), el que expones es un cambio de variable de traslación.
Se puede hacer de dos formas, realizas el cambio de variable directamente cuando quieres obtener la distribución acumulada o bien, realizas el cambio a lo último.
Como aquí (un poco más arriba) en la parte de comentarios ya hay un ejercicio de cambio de variable resuelto directamente, éste lo haremos de la otra forma (que creo que es más sencillo).
Empezamos: Obtenemos la función de distribución acumulada de la variable aleatoria X (es una integral sencilla, así que te pongo directamente la solución):
· F(x) = (1/2)x³
Ahora, realizaremos el cambio de variable, mediante la propia definición de la distribución acumulada:
· F(Y) = P(Y ≤ y)
Teniendo en cuenta que: Y = 3 - X.
· F(Y) = P(Y ≤ y) = P(3-X ≤ y) = P(X ≥ 3-y) = 1 - P(X < 3-y) = 1 - Fx(3-y)
Sustituimos:
· F(Y) = 1 - (1/2)(3-y)³ = 1 + (1/2)(y-3)³
Ahora, queda determinar el intervalo de acción, para ello debemos obtener los dos límites, el que haga cero y el que haga uno a la función de distribución acumulada.
Igualamos y obtenemos los resultados:
· Si y ≤ 1.740079:.........F(x) = 0
· Si 1.740079 < y < 3:.....F(x) = 1 + (1/2)(y-3)³
· Si y ≥ 3:................F(X) = 1
Una vez obtenida la función de distribución acumulada, podemos obtener la función de densidad con la siguiente relación:
· f(y) = F'(y)
Realizamos dicho cálculo y obtenemos:
· f(y) = (3/2)(y-3)²
Para el intervalo: 1.740079 ≤ y ≤ 3.
Existe un método (de teoría) que te marca el camino a seguir, te ahorras varios pasos pero te tienes que aprender el método.
Un saludo y gracias por tu comentario.
Me quedó clarísimo!... muy bien explicado.
Muchas, Muchas Gracias!!!
Hola, muy bueno tu blog, señor manuel para que me ayude o me oriente a realizar un ejercicio:
El tiempo hasta la falla de un equipo sigue una distribucion exponencial con una media de 500 dias, los costos del mantenimiento preventivo y del mantenimiento de fallas son de 50 y 300 dolares respectivamente.
Determine (tp), el momento optimo para el reemplazo preventivo.
Muchas Gracias de Ante mano
Saludos desde Venezuela
Buenas:
El ejercicios que expones necesita de cierta teoría previa:
· ¿Qué es un mantenimiento preventivo?.
· ¿Qué es un mantenimiento de fallas?
· ¿Qué es el momento óptimo para reemplazo?
En otras palabras, no es un ejercicio de estadística sino de una aplicación que se basa en la estadística pero que previamente, se necesita de conceptos previos para poder ser resuelto.
· PD: Por cierto, para un mantenimiento preventivo no tiene mucho sentido una exponencial (si no recuerdo mal), más bien una distribución de Weibull.
Un saludo y gracias por tu comentario.
Hola me gustaria por favor si me podrian ayudar con este ejercicio es que me hago un lío, el enunciado es el siguiente:
Las puntuaciones obtenidas por un grupo de alumnos en un test sigue una distribuición normal con media 24. Sbiendo que el 25% de los alumnos consiguen menos de 21.3020, podemos afirmar que el 10%consigue mas de:
A)29.1262
B)Ninguna de las otras respuestas
C)26.6979
D)25.3489
Muchas gracias de antemano ^^
Hola señor Manuel muy buena su pagina me ha ayudado un monton =) querría pedirle haber si me puede ayudar con este ejercicio por favor:
Si queremos aproximar la distribución binomial(100,0.2) por una distribución normal¿ Cuál sería la más adecuada?
Opcion 1: N(20,16)
Opcion 2:(100, 2)
Opcion 3:(100,0.2)
Opcion 4: No es ninguna de las anteriores soluciones
Buenas:
Realizamos una recopilación de los datos que nos ofrece el problema:
· X ≡ 'Puntuaciones obtenidas por un grupo de alumnos en un test'.
Se sabe que (por el enunciado del problema): X~N(24, σ).
En este problema, debemos obtener el valor de la varianza para poder resolver los que nos piden, para ello, nos apoyamos sobre la primera observación:
· P(X < 21.3020) = 0.25
Tipificamos:
· P(X < 21.3020) = P(Z < (21.3020 - 24)/σ) = 0.5 + Φ(z) = 0.25
Despejamos: Φ(z) = 0.25 - 0.5 = -0.25.
Valor negativo pero no nos debe preocupar, ya que la campana de Guass es una curva simétrica, por lo tanto, buscamos en tablas el valor 0.25.
Si lo hacemos, veremos que no existe un valor exacto para tal dato, por lo que realizamos una interpolación lineal:
0.67.........Z.....0.68
0.2486...0.25...0.2517
· Z = [(0.67-0.68)(0.2486-0.25)/(0.2517-0.2486)] + 0.67 ≈ 0.674516
Por lo tanto: z = -0.674516 (negativo porque hay que recordar que el valor inicial era negativo).
Ahora podemos sustituir valores:
(21.3020-24)/σ > -0.674516
Despejamos el valor que nos interesa:
· σ < 3.999905
Llegados a este punto, ya tenemos todos los datos necesarios: X~N(24, 3.999905).
Ahora, podemos obtener el dato que nos piden:
· P(X > x) = 1 - P(X ≤ x) = 0.1
Despejamos: P(X ≤ x) = 1-0.1 = 0.9
Tipificamos:
· P(X ≤ x) = P(Z ≤ (x-24)/3.999905) = 0.5 + Φ(z) = 0.9
Despejamos: Φ(z) = 0.9-0.5 = 0.4.
Buscamos en tablas el valor 0.4, veremos que no existe un valor exacto para tal dato, por lo que realizamos una interpolación lineal:
1.28.........Z.....1.29
0.3997...0.40...0.4015
· Z = [(1.28-1.29)(0.3997-0.40)/(0.4015-0.3997)] + 1.28 ≈ 1.281667
Ahora podemos sustituir valores:
1.281667 ≤ (x-24)/3.999905
Despejamos y obtenemos la solución al problema: x ≥ 29.126546.
Un saludo y gracias por tu comentario.
Buenas:
Para aproximar una distribución binomial a la normal, sólo debemos realizar los pasos que nos dicta la teoría, es decir, primero, comprobar que realmente se puede realizar dicha aproximación, para ello es necesario que cumplan las siguientes condiciones:
1. n·p ≥ 5: 100·0.2 = 20 ≥ 5 OK.
2. n·q ≥ 5: 100·(1-0.2) = 80 ≥ 5 OK.
Se cumplen las condiciones necesarias, ahora, podemos realizar la aproximación:
· B(100, 0.2) ---> N(μ, σ)
Pues bien, hacemos los cálculos:
· μ = n·p = 100·0.2 = 20
· σ² = n·p·q = 100·0.2·(1-0.2) = 16
Por lo tanto, la aproximación es:
· B(100, 0.2) ---> N(μ, σ) = N(20, √16) = N(20, 4)
La solución sería: Opción 4: No es ninguna de las anteriores.
Ahora bien, en ciertos colegios, institutos, universidades, etc, la nomenclatura es algo distinta:
· B(100, 0.2) ---> N(μ, σ²) = N(20, 16)
Por lo tanto, la solución sería: Opción 1.
Depende de la nomenclatura que uses, será una u otra.
Un saludo y gracias por tu comentario.
Sea X una variable aleatoria normal de media 5 y desviación típica 2. Entonces
a. P(X>2) = 0.93319
b. P(X>2) = 0.5
c. Ninguna de las otras respuestas.
d. P(X>2) = 0.06681
me podrias ayudar x favor....
gracias anticipadas!
Sea X una variable aleatoria que sigue una distribución normal con media 64 y varianza 16. Determinar el valor de la constante a que verifica P(x < a)=0.1586553
a. 68
b. Ninguna de las otras respuestas.
c. 60
d. 48
gracias anticipadas....me vendria muy bien una ayudita...
hola haber si me puedes echar una manita con esto, gracias:
Las puntuaciones obtenidas por un grupo de alumnos en un test de aptitud, sigue una distribución normal con media 24. Sabiendo que el 25% de los alumnos consiguen menos de 20.62755, podemos afirmar que el 90% consigue más de:
a.Ninguna de las otras
b.17.59224
c.30.40776
d.26.6979
Buenas:
Esta respuesta va dirigida a las tres anteriores (supongo que las ha escrito la misma persona).
Respecto al primer ejercicio que propones, es un caso típico de normalización de una variable aleatoria continua, te recomiendo que te veas el capítulo de la tabla de la Normal dónde se explica cómo normalizar variables de este tipo. En caso que no quieras, pues tienes una cantidad de problemas resueltos que podrás ver cómo se hace, por ejemplo: Problema 11.
Respecto al segundo problema, otro caso típico de manejar la distribución Normal, vuelves a tener a tu disposición todos los problemas aquí resueltos, por ejemplo: Problema 17.
Y respecto al último ejercicio, sólo tienes que mirar cuatro comentarios atrás y encontrarás uno de las mismas características resuelto, simplemente tienes que cambiar los datos.
Que yo os resuelva los ejercicios no significa que aprobéis, tenéis que poner de vuestra parte y para ello, estudiar un mínimo de teoría y por supuesto, hacer problemas.
Y precisamente es lo que en este blog, Aqueronte, podrás encontrar.
Un saludo y gracias por tu interés.
Hola buenas, podrias decirme cual es el resultado exacto de estos problemas? Esque no se como hacerlos :S
Sabemos que el 30% de las personas que residen en una determinada ciudad son solteras. Supongamos que seleccionamos al azar cinco personas de esta población. ¿Cuál es la probabilidad de que al menos tres estén casadas?
a. 0.83692
b. 0.16308
c. 0.3087
d. Ninguna de las otras respuestas
Y de este:
Una distribución uniforme en el intervalo (a,b) tiene de media 3, y de varianza 1/3. Lo valores de a y b han de ser:
a. a=0, b=6
b. Ninguna de las otras respuestas.
c. Es imposible calcular a y b con tan pocos datos
d. a=2, b=4
Y por ultimo:
Se ha comprobado que la duración de las conversaciones telefónicas urbanas sigue una distribución exponencial con media 5 minutos. Calcular la probabilidad de que una llamada tenga una duración comprendida entre 3 y 9 minutos.
a. 0.3835127
b. 0.3669673
c. 0.3200259
d. Ninguna de las otras respuestas.
MUCHAS GRACIAS !
Buenas:
Te resuelvo el primer problemas que planteas.
Para empezar, es un problema de variables aleatorias discretas (NO continuas). Teniendo claro lo anterior, pasamos a definir los sucesos:
· S ≡ 'Personas que son solteras'.
· N ≡ 'Personas que no son solteras'.
· P(S) = 0.3
· P(N) = 1-P(S) = 1-0.3 = 0.7
· X ≡ 'Nº de personas que no son solteras que residen en una determinada ciudad'.
La variable aleatoria discreta X sigue una distribución Binomial de parámetros: X~B(5, 0.7)
La probabilidad que debemos obtener es el siguiente:
· P(X ≥ 3) = 1 - P(X < 3) = 1 - [P(X=0) + P(X=1) + P(X=2)] = 0.83692
No he sustituido valores ya que por comentarios no se vería bien (ya que no puedo poner subíndice ni superíndice (te puedes mirar cualquier problema del capítulo: Variable Aleatoria Discreta y Distribuciones de Probabilidad, por ejemplo el Problema 51).
Por lo tanto, la solución sería la a.
Respecto al segundo problema, simplemente debes emplear las expresiones matemáticas de la media y desviación típica de la distribución Uniforme y tendrás dos ecuaciones con dos incógnitas, fácil de resolver, te puedes mirar un ejercicio que tenemos parecido: Problema 57.
Y respecto al tercer problema, un ejercicio típico y fácil de manejar una distribución exponencial, te puedes mirar el siguiente ejemplo: Problema 73.
Una pregunta, ¿no sabes hacer éstos ejercicios o es que ni siquiera lo has intentado?
Un saludo y gracias por tu interés.
Dada la función:
f(x):
ax^2 , 1<= x <=3
0 , en otro lugar
** Hallar "a" para que f sea de densidad y graficar f y F.
** Calcular p(x>=2); E(x) y V(x)
Donde
E(x) = Esperanza
V(x) = Varianza
Buenas StoneCr1s:
Desde el ejercicio 1 hasta el 10 mínimo, encontrarás problemas de carácter similar al que expones e incluso, de mayor dificultad.
Un saludo y gracias por tu comentario.
Buen Dia Manuel: Felicidades por tu blog,me ha servido mucho en mis clases, me gustaria consultarte en el problema 57, porque se tomo el valor de √3 o de donde se obtuvo este valor?estot tomando este ejercicio para resolver un ejercicio similar, pero me siento confundida sobre ese valor √3. Gracias por tu ayuda.
Renata
Buenas Renata:
El √3 viene de simplificar el sistema de dos ecuaciones, te lo resuelvo para que lo veas. Tenemos dos ecuaciones con dos incógnitas (a y b), son las siguientes:
· a + b = 20
· b - a = √12
Operamos un poco con ellas:
· a = 20 - b
· b = √12 + a
Ahora, podemos sustituir la segunda ecuación en la primera para obtener el valor de la incógnita a:
· a = 20 - √12 - a
Agrupamos:
· 2a = 20 - √12
Despejamos:
· a = 20/2 - √[12/4] = 10 - √3
Fíjate que el 2 que está dividiendo entra en la raíz elevado al cuadrado.
Por eso se obtiene en parámetro √3.
Un saludo y gracias por tu comentario.
Hola Manuel:Te saludo desde Nicaragua, felicidades por tu blog, me ha sido muy util, casi no entendia los temas en clases, tus ejemplos me han ayudado muchisimo para aclarar mis dudas,deseo pedirte ayuda con un ejercicio, he estado intentado resolverlo,pero me ha dado bastantes problemas, el ejercicio es una profesora desea conocer si el porcentaje de aprobados en su asignatura ronda el 60% para comprobar si se cumplen los objetivos presupuestos al inicio del curso. Para comprobarlo reviso las calificaciones de 100 estudiantes, de los que obtuvo un porcentaje del 57% de aprobados. Con un margen del error del 5% que valor toma el estadistico? Se puede rechazar la hipotesis de partida?
Agradezco de antemano tu ayuda.Saludos cordiales.
Roberto Carlos M.
Buenas Roberto Carlos:
El problema que planteas no es de Variables Aleatorias Continuas sino que corresponde a Pruebas de Hipótesis o Intervalos de Confianza.
Resolverlo por este apartado de comentarios, será bastante tedioso (por la nomenclatura de las ecuaciones a plantear), a parte, me parece interesante el dato del error que plantea el enunciado del problema, así que, lo he resuelto y añadido como problema de boletín al apartado que le corresponde: Estimación, Intervalos de Confianza y Pruebas de Hipótesis que podrás encontrar en el curso de Estadística.
El problema concreto es el número 83 (Enlace: http://unbarquero.blogspot.com/2011/12/problema83-estimacion-y-pruebas-de.html)
Un saludo y gracias por tu comentario.
Muy buen blog, tienen muy buenos contenidos y muy buenos ejemplos, me gustaria pedir me ayudaran con un ejercicio:
Dos profesores A y B dieron en un centro, dos cursos de la misma asignatura. La distribución de las notas de sus alumnos reflejó los siguientes resultados a lo largo de los diez últimos años. Profesor A: media 5 y desviación típica 3. Profesor B: media 5 y desviación típica 1. En el presente curso un alumno que sólo conoce estos datos y que aspire a una nota de 9 ó 10, ¿con qué profesor debería matricularse?
Gracias.
Buenas:
Lo primero es hacer una recopilación de los datos que nos ofrece el enunciado del problema:
· A ≡ 'Nota obtenida por el profesor A'.
· B ≡ 'Nota obtenida por el profesor B'.
Ambos ejercen la misma asignatura y suponemos que dichas variables aleatorias siguen una Distribución Normal, por lo tanto:
· A~N(5, 3)
· B~N(5, 1)
La probabilidad que debemos obtener es la siguiente:
· P(9 ≤ X ≤ 10)
Siendo:
· X ≡ 'Nota obtenida por un alumno'.
Pues ya tenemos concretados todos los datos del problema, lo que nos falta hacer es obtener la probabilidad anterior respecto a cada profesor.
· Para el Profesor A:
P(9 ≤ X ≤ 10) = P[(9-5)/3 ≤ Z ≤ (10-5)/3] ≈ P(1.33 ≤ Z ≤ 1.67) = Φ(1.67) - Φ(1.33)
Buscamos en la tabla de la Normal y sustituimos valores:
P(9 ≤ X ≤ 10)≈ P(1.33 ≤ Z ≤ 1.67) = Φ(1.67) - Φ(1.33) = 0.4525 - 0.4082 = 0.0443
Por lo tanto, la probabilidad de obtener una nota entre 9 y 10 matriculándose en la asignatura impartida por el profesor A es de 0.0443.
· Para el Profesor B:
P(9 ≤ X ≤ 10) = P[(9-5)/1 ≤ Z ≤ (10-5)/1] = P(4 ≤ Z ≤ 5) = Φ(5) - Φ(4)
Buscamos en la tabla de la Normal y sustituimos valores:
P(9 ≤ X ≤ 10) = P(4 ≤ Z ≤ 5) = Φ(5) - Φ(4) ≈ 0.5 - 0.5 = 0
Por lo tanto, la probabilidad de obtener una nota entre 9 y 10 matriculándose en la asignatura impartida por el profesor B es de 0.
Evidentemente, la probabilidad de obtener una nota entre 9 y 10 es mayor si el alumno se matricula con el profesor A.
· PD: Aparte, en mi opinión, el alumno debería apuntarse a clases particulares o estudiar bastante por su cuenta ya que la nota media de ambos profesores para su asignatura es de 5.
Un saludo y gracias por tu comentario.
Hola Manuel:Gracias por tu ayuda con este ejercicio,me ha quedado claro , y estoy de acuerdo contigo que el alumno debera optar por tutorias o estudiar bastante si desea obtener una nota arriba de 5. Te comento que en el ejercicio se dan varias opciones a escoger:
a. Con ninguno de los dos, pues no puede sacar más de 8.
b. Con el A.
c. Con el B.
d. ninguna de las anteriores.
Segun mi criterio y la ayuda que tu me haz proporcionado,en la tarea que presente opte por la opcion b, ya que aunque la nota media de ambos profesores sea de 5,no es imposible que un estudiante obtenga mas de 8,claro si se esfuerza y estudia mucho,gracias por tu ayuda.
Hola este blog es un exito, me ha servido grandemente, queria consultar que significa la siguiente expresion:
F0+d(F(x)) dx = 1 .Esta expresion la mencionan en el material de mi clase de Estadistica en el tema de funciones de distribucion de una variable aleatoria continua, pero no me queda claro que significa.
Gracias por su ayuda.
Daniel Moreno/Honduras
Buenas:
Hombre, con el profesor A tiene una probabilidad de estar entre las notas sugeridas, eso sí, la probabilidad es baja.
-----------
La ecuación que mencionas:
· F0 + d(F(x))dx = 1
No es más que una de las dos condiciones que debe cumplirse para que una función sea una función de densidad de probabilidad.
Sólo que está escrita de diferente manera, en el blog empleamos la integral (para ver ambas condiciones debes irte al principio de la teoría que exponemos en este capítulo).
Pero ambas son equivalentes, ya que si despejas en tu expresión F(x) te dará en función de la integral tal y cómo lo tenemos nosotros definido.
Un saludo.
IMPRESIONANTE blog
muy muy útil
felicidades y gracias
:)
Hola, por favor necesito ayuda con estos ejercicios...
_La primera de probabilidad:
51%posee fondo solidario
34 posee beca de alimentación
50 de dinero
8 solo beca de alimentacion
22 solidario y alimentación
36 posee solidario pero no beca de alimentacion
3 solidario y dinero pero no de alimentacion
preguntas la probabilidad de :
1 no posee nada
2 solo uno
3 posee fondo y beca de dinero , si tiene beca de alimentacion
4 posee fondo solidario o beca de dinero
5 no posee beca de alimentación
6 posee beca de dinero sabiendo que posee solidario
problema 2 dice mas o menos asi:
alumnos del colegio X postularon 40 a la especialidad A , 35 a la B 25 a la C. y en años anteriores onda se hizo un historial y el 40%, 70%, y 20% participaron en el proceso de postulacion de la prueba. Cual es la probabilidad de q de los alumnos q no postularon sean de la especialidad B?
3...el curso tiene un promedio d 2.4 inasistencia por día cual es la probabilidad :
a) un curso resistre en un día mas de 5 inasistencia
b) de 10 cursos se observe que en 3 ahi dos inasistencias
4 en un colegio el 75% provienen de un campamento :
Si se consideran 15 alumnosi( n =15) cual es la probabilidad que por lo menos 12 provienen del campamento.
si( n= 480) probabilidad de que menos de 300 provengan del campamento
5 te dice que de distribucion normal de u=3,5 desviacion standar=0,8 habla de la distancia con respcto a un colegio
a) probabilidad de que por lo menos residan dos
b) prob. de que 5 alumnos queden en menos de 4 km
Buenas Moira:
¿Qué tipo de ayuda necesitas? Has puesto varios ejercicios de una temática diferente, desde probabilidad hasta variables aleatorias continuas.
En el apartado de Estadística, puedes entrar en los distintos capítulos y hacer o revisar cada ejemplo que podrás encontrar, dónde seguramente, la mayoría de los problemas que expones aquí, están resueltos en su correspondiente categoría (o problemas muy similares).
Si después de esto sigues teniendo dudas sobre un ejercicio concreto (o varios), escribe en el apartado correspondiente al capítulo de Estadística dónde podré ayudarte.
Un saludo.
3. Un curso tiene un promedio d 2.4 inasistencia por día ¿cual es la probabilidad :
a) un curso registre en un día mas de 5 inasistencia (aplicacion de distribucion binomial?)
b) de 10 cursos se observe que en 3 hay 2 inasistencias ( será binomial tambien?)
4. En un colegio el 75% de los alumnos provienen de un campamento:
a)Si se consideran 15 alumnos ¿cual es la probabilidad que por lo menos 12 provengan del campamento? (BINOMIAL)
b)si se tienen 480 alumnos cual es la probabilidad de que menos de 300 provengan del campamento
(SERA NORMAL?)
5. La distancia a la que viven los alumnos de su colegio en Km se rige por la distribución normal de u=3,5 y desviación estándar=0,8 . ¿cuál es la probabilidad de:
a) de que un alumno resida por lo menos a 2km del colegio (aplicacion de distribucion normal)
b) probabilidad de que 5 alumnos vivan a menos de 4 km (NO ENTIENDO)
Buenas Moira:
Respecto al ejercicio número 3:
· Apartado a) Se debe resolver mediante una Distribución de Poisson.
· Apartado b) Hipergeométrica.
Respecto al ejercicio número 4:
· Apartado a) Distribución Binomial
· Apartado b) Es Binomial pero debido al tamaño, se deberá comprobar si se puede aproximar a la Distribución Normal (en caso contrario, comprobar compatibilidad con la Poisson).
Respecto al ejercicio número 5:
· Apartado a) Distribución Normal (te lo indica el enunciado del problema).
· Apartado b) Distribución Binomial, tenemos tanto la media cómo la desviación estándar, por lo que tendremos dos ecuaciones con dos incógnitas para obtener los parámetros necesarios de la Binomial.
Un saludo.
Hola me ha servido de mucha ayuda leer el blog, todas las respuestas aclaran conceptos que necesitaba.
Necesito ayuda con este ejercicio, es de examen y no encuentro ninguno parecido..
Se considera q el numero diario de ejemplares venido en un kiosko de una revista de motor es de media 25(Poisson), calcula la probabilidad de q los ingresos obtenidos durante 60 dias esten entre 3780€ y 3900€.
Gracias de antemano.
Buenas Ana:
En el problema falta un dato, ¿cuánto es el precio por unidad de revista? En otras palabras, ¿cuánto vale la revista?
Si te das cuenta, el problema pide obtener una probabilidad acorde a beneficios, en cambio, tal como tú lo has redactado, el problema sólo nos habla de la media de revistas vendidas en un día.
Problemas similares tenemos en este blog, por ejemplo, los de éste capítulo:
· Problema 77
· Problema 79
· Problema 56
· Problema 58
Y algunos más. Aún así, voy a exponer la manera de resolverlo a expensas del precio por revista.
Primer paso, definir nuestra variable aleatoria:
· X ≡ 'Número diario de ejemplares vendidos en un kiosko de una revista de motor'
Dicha variable sigue una distribución de Poisson, X~P(25) ejemplares vendidos/al día.
El problema quiere hacer un estudio durante 60 días, por lo que tendremos que adaptar nuestro parámetro promedio:
· 1 --- 25
· 60 --- λ
Por lo tanto, el número medio de ejemplares vendidos/60 días es:
· λ = (60·25)/1 = 1500
La probabilidad que debemos obtener es la siguiente:
· P(3780 ≤ Y ≤ 3900)
Y como podemos comprobar, la variable aleatoria Y no es la misma que nuestra variable aleatoria X. La variable aleatoria Y se describiría de la siguiente manera:
· Y ≡ 'Ingresos obtenidos durante 60 días de ejemplares vendidos en un kiosko de una revista de motor'
Para que nuestra variable aleatoria X pase a ser la variable aleatoria Y, tendríamos que tener el precio por unidad del ejemplar que se vende en el kiosko.
Aún así, vamos a seguir con el ejercicio. Nuestra variable aleatoria es del tipo discreta, determinaremos, si se puede aproximar a la Normal, para ello, se deben cumplir la siguiente condición:
1. λ > 25 → 1500 > 25 OK.
Por lo tanto: X ~ N(λ, √λ) = N(1500, √1500).
Aplicamos el factor de corrección:
· P(3779.5 ≤ Y ≤ 3900.5)
Y vamos a suponer, un par de casos.
· Primer Caso
La revista se vende por un euro la unidad.
Por lo tanto, ya transformar nuestra variable aleatoria a la que necesitamos de la siguiente manera:
· Y = X·n = 1500·1 = 1500
Donde n, es el precio por unidad de revista vendida.
Por lo tanto, tipificamos:
· P(3779.5 ≤ Y ≤ 3900.5) = P[(3779.5 - 1500)/√1500 ≤ Z ≤ (3900.5 - 1500)/√1500] ≈ P(58.86 ≤ Z ≤ 61.98)
Buscando en la tabla de la Normal, obtenemos la solución:
· P(3779.5 ≤ Y ≤ 3900.5) ≈ P(58.86 ≤ Z ≤ 61.98) = Φ(61.98) - Φ(58.86) = 0.5 - 0.5 = 0
Es decir, que si la revista se vende a un euro por unidad, la probabilidad de que los ingresos obtenidos durante 60 días estén comprendidos entre 3780€ y 3900€ es de cero.
· Segundo Caso
La revista se vende por dos euros y medio la unidad.
Por lo tanto, ya transformar nuestra variable aleatoria a la que necesitamos de la siguiente manera:
· Y = X·n = 1500·2.5 = 3750
Donde n, es el precio por unidad de revista vendida.
Por lo tanto, tipificamos:
· P(3779.5 ≤ Y ≤ 3900.5) = P[(3779.5 - 3750)/√3750 ≤ Z ≤ (3900.5 - 3750)/√3750] ≈ P(0.48 ≤ Z ≤ 2.46)
Buscando en la tabla de la Normal, obtenemos la solución:
· P(3779.5 ≤ Y ≤ 3900.5) ≈ P(0.48 ≤ Z ≤ 2.46) = Φ(2.46) - Φ(0.48) = 0.4931 - 0.1844 = 0.3087
Es decir, que si la revista se vende a dos euros y medio por unidad, la probabilidad de que los ingresos obtenidos durante 60 días estén comprendidos entre 3780€ y 3900€ es de 0.3087.
Un saludo.
como puedo diferenciar una variable aleatoria continua de una discreta.por ejemplo:
La pérdida de peso que se logra con cierta dieta.
Tiempo que tardan en entregar una pizza desde el momento en que se ordena.
Quisiera consultarte como se resuelve este ejercicio ya que observe todo los ejercicios que propusiste y no hay uno similar :
Se observó durante un largo período que la cantidad semanal gastada en
mantenimiento y reparaciones en cierta fábrica tiene aproximadamente una
distribución normal con media 160000 pesos y desviación estándar 28000.
a) Si el presupuesto para la próxima semana es de 180000 pesos. ¿Cuál será la
probabilidad que los costos reales sean mayores a la cantidad presupuestada?
b) ¿De cuánto tendría que ser el presupuesto para reparaciones semanales, para
que la cantidad presupuestada solamente se sobrepase con una probabilidad
igual a 0.1?
c) Se sabe que en una semana el gasto no superó los 150000 pesos. ¿Cuál será la
probabilidad que haya superado los 120000 pesos?
d) Si se elijen aleatoriamente del período de observación 4 semanas. ¿Cuál es la
probabilidad que por lo menos en 3 de ellas el gasto en mantenimiento en
reparaciones se encuentre entre 120000 y 150000 pesos?
Graxias
Buenas:
@José Luis: Para diferenciar entre una variable aleatoria contínua de una discreta es 'relativamente' fácil.
· La variable aletoria continua tiene infinitos posibles valores dentro d eun intervalo definido.
· La variable aleatoria discreta, tiene un conjunto de valores finitos para los cuales está realizado el experimento.
Por ejemplo, las veces que se lanza un dado, es una variable aleatoria discreta ya que el experimento se realiza un número finito de veces (el lanzar un dado).
En cambio, las definiciones que has puesto podían ser variables aleatorias continuas, simplemente falta definir el intervalo.
@Anónimo: Creo que no vistes todos los ejercicios (es más), podría decirte que no has visto ninguno, ya que hay un montón de ellos que se resuelven de manera similar al que has puesto, tipificar la variable aletoria continua a la Normal.
Como referencia están los siguientes:
· Apartado a) --> Problema 15
· Apartado b) --> Problema 32
Para el Apartado c) es similar que el Apartado a)
Revísalos y las dudas que tengas, pregúntalas.
Gracias por vuestros comentarios.
Hola queria consultarte sobre este ejercicio:
Sea X una variable aleatoria con funcion de densidad dada por:
f(x)= 0.2 si -1≤x<0
0.2+cx si 0≤x<1
0 en otro punto
Calcular el valor de c
Mi duda es si debo igualar la suma de las dos integrales a 1, o si debo igualar cada integral a 1, para luego poder despejar c.
Espero tu respuesta. Gracias!
Buenas:
Debes igualar a 1 la suma de ambas integrales, ya que es esa la función que define la variable aleatoria.
Tienes un par de ejemplos en los ejercicios (son parecidos, no exactamente obtener el valor de un parámetro par cumplir que sea una función de densidad):
· Problema 31
· Problema 39
Un saludo.
Buenas tengo un problema con este ejercicio el cual no se resolver...
sea Z una variable aletatoria distribuida normalmente con media cero y desviacion estandar uno. Encontrar la funcion que genera momentos Z´
Buenas:
No te puedo ayudar con tu problema ya que no damos soporte en el cálculo de momentos, aún así, decirte que su obtención no es difícil, plantea la integral mediante su definición y deberás resolverla.
Quizás, en un futuro, ampliemos el apartado de Estadísticas con nuevos temas: Distribuciones multivariables, Estudios no paramétricos, obtención de momentos, etc.
Un saludo.
Buenas tardes, me podria ayudar a resolver este ejercicio:
Sea X una variable aleatoria con funcion de densidad f(x)=(3x(2-x))/4 si o<x<2; y sea y=x^2. Calcular E(y)
Muchas gracias :)
Buenas:
Podrás encontrar ejercicios parecidos al que propones en el apartado de los problemas.
Concretamente, el siguiente ejercicio, en el Apartado a), se detallan los pasos a seguir para obtener la solución del problema:
· Problema 69: Apartado a)
Si tienes algún problema en la resolución, estamos aquí para ayudarte.
Un saludo.
Hola buenos dias, tengo un problema con un ejercicio y por mas que lo intento no se por donde empezar,el problema es el siguiente:
Se quiere analizar la rendibilidad que tienen determinadas lineas aereas. Se analiza la información sobre el grado de ocupación de los aviones durante 3 meses, para 4 lineas diferentes: Madrid-Oviedo, Barcelona- Dublin, Reus- Venecia y Girona-París. Las medianas muestrales obtenidas a partir de 100 vuelos analizados a cada ruta muestran el siguiente porcentaje de ocupación: 60,68,45 y 76. La desviación estandar es de 20 y es la misma para todas las rutas.
a. Suponemos que el llindar de ocupación a partir del qual se considera que los viajes resulten rentables es el 68%, construir un intervalo para la mediana mostral que contenga el 95% de los casos, i compararlo con el llindar. ¿Cuales son las lineas que de podrian considerar como rentables?
b. Teniendo en cuenta que la mediana de ocupación de la ruta Reus-París es del 33%, ¿cual tendria que ser la medida muestral si quisieramos asegurar, con una probabilidad del 95%, que la ocupación mediana sea superior al 40%?
Haber si me podeís hechar una mano, muchas gracias.
Buenas:
Antes que nada pedirte que expongas tus preguntas en el sitio adecuado, tu pregunta no corresponde a este capítulo sino más bien al correspondiente de Estimación y Pruebas de Hipótesis (más que nada para que esté todo lo más ordenado posible, esto nos ayuda a todos).
Dicho esto, ya te he dado una pista, en el Apartado a) debes obtener un intervalo de confianza para la media de cada una de las rutas.
En este caso, los cuatro intervalos de confianza al 95% que debes realizar, son del tipo Normal (con un tamaño de muestra mayor o igual a 30 y con desviación estándar conocida), en el apartado correspondiente que te he mencionado anteriormente, encontrarás multitud de ejercicios similares, aquí un ejemplo:
· Problema 38.
La forma de abordar tu problema es muy parecida en ambos apartados al problema que te he expuesto anteriormente.
Con respecto a qué líneas se pueden considerar rentables, éstas serán las que en su intervalo de confianza obtenido esté la cifra 0.68 recogida.
· PD: ¿Eres hispano hablante? Me explico, hay ciertas palabras que no entiendo o el concepto es distinto, tal como en tu Apartado b) te refieres a la mediana, realmente quieres decir la media.
Un saludo.
Hola,
Tengo algunas dudas, si tienes la funcion de densidad: f(x)= 1/2 e^(-|x|)
Como se halla:
P(|x|+|x-3|≤3)
P(x^3-x^2-x-2≤0)
P(exp(senπx)≤1)
P(x "perteneciente a" R-Q)
Saludos :)
Buenas:
Lo primero que tienes que comprobar es que la función dada cumple las condiciones de que sea una función de probabilidad, éstas condiciones son dos:
1. f(x) > 0, para todo x. La cumple.
2. int_a^b{f(x)dx} = 1. La cumple.
La primera condición es fácil obtenerla, sustituye valores (el que quieras de x), y comprobar que el resultado es positivo.
Para la segunda, deberás realizar la integral entre los intervalos - infinito y + infinito, dónde obtendrás el resultado de 1 (por lo tanto, también la cumple). Te dejo el resultado por wxMaxima:
>> integrate(0.5*%e^(-abs(x)), x, -inf, inf);
>> 1.0
Ahora bien, al tener un módulo de la variable x, lo que obtendremos es una función simétrica (valores positivos y negativos), si consideramos sólo los valores positivos tendremos la siguiente función de probabilidad acumulada:
· Para x ≤ 0: F(x) = 0.5
· Para 0 < x < ∞: F(x) = 0.5 + 0.5·(1 - e^(-x))
· Para x ≥ ∞: F(x) = 1
Como verás, ese 0.5 viene de la parte simétrica de la curva que contiene los valores negativos de la variable aleatoria continua x.
Un saludo.
q tal, permiteme humildemente felicitarte esta muy bueno tu blog.
porfavor nesecito ayuda en este problema y anticipadamente agradecerte por la ayuda:
el punto “A” se ubica aleatoriamente sobre una línea recta donde se sabe que la distancia del punto “P” al punto fijo “O” se distribuye normalmente con media y desviación estándar ambos parámetros conocidos ( u y ç). Se requiere ubicar 3 puntos A, B, C en la línea indicada en tales posiciones que el valor esperado del mínimo de las 3 distancias absolutas /AP/, /BP/, /CP/ sea un mínimo. ( Valor esperado de la distancia absoluta de P a la ubicación más próxima de A; B y C debe ser mínimo). Asumiendo q B se ubica en la posición esperada de P (osea OB=e,epsilo) encuentre las posiciones optimas de A Y C. considere AB=BC=Y y BP=X
Muchas gracias por el blog, me esta ayudando mucho a preparar los exámenes, bueno quería pedirte ayuda para resolver este problema:
La venta diaria de una fábrica de montaje de ordenadores se adapta a una distribución
uniforme entre 20 y 40 unidades.
a) Después de transcurridos 182 días de venta, ¿cuál es la probabilidad de haber vendido
más de 5.600 ordenadores, suponiendo las ventas independientes de un día para
otro?.
b) ¿Cuántos días de venta debemos considerar para asegurar, con un 67% de
probabilidad, la venta de más de 6.000 unidades?
Buenas:
La variable aleatoria continua sigue una distribución Uniforme de parámetros: 20 y 40 unidades al día.
El problema te menciona la cantidad de unidades fabricadas en 182 días que son de 5600 unidades.
Para obtener la respuesta a este apartado, vamos a guiarnos con la condición que el enunciado del problema nos ha propuesto: las ventas son independientes unas de otras.
· ¿Qué quiere decir esto? Pues lo que se venda en un día no interfiere con los demás días de venta.
Teniendo esto claro, lo que tenemos que hacer es adecuar la variable a los datos de nuestra variable aleatoria continua, es decir, cuanto vende en un día.
· 5600/182 ≈ 30.769231
Por lo tanto, la probabilidad que debemos obtener es la siguiente:
· P(X > 30.769231) = 1 - P(X ≤ 30.769231).
El siguiente apartado, debemos obtener los días necesarios para obtener unas ventas de más de 6000 unidades al 67%, como verás, se siguen los mismos pasos que en el anterior apartado pero esta vez, debemos calcular los días necesarios para cumplir la condición dada.
Un saludo.
Hola necesito ayuda con este ejercicio de estadística:
Una variable aleatoria discreta Y tiene la siguiente distribución:
P(Y=1)=1/2
P(Y=2)=1/4
P(Y=3)=1/4
a)Encuentre la función de distribución acumulada F(y)=P(Y< o =y).Asegúrese de que para todos los valores reales de y,se tenga un solo valor para F(y).
b) Encuentre las siguientes probabilidades:
P(Y < 1) = ?
P(Y 1) = ?
P(Y < 2) = ?
P(Y > 2) = ?
P(Y 3) = ?
P(Y 3) = ?
Buenas:
Para empezar decirte que el ejercicio que propones es del apartado de Variables Aleatorias Discretas (NO el de Variables Continuas), por lo que de aquí en adelante, le pediría que cada ejercicio o duda se publique en el apartado correspondiente (así todo estará ordenado y será de ayuda a todo el mundo).
Respecto a su ejercicio, en el apartado de Variables Aleatorias Discretas, concretamente en los ejercicios 2 y 4, encontrarás el procedimiento de como resolver el ejercicio que usted propones.
Un saludo.
Voy a intentar escribir de nuevo el problema a ver si sale:
La superficie en hectáreas de los socios de una cooperativa olivarera se distribuye con la siguiente f.d.d.:
f(x) = (10/385)*(1+x) si 1<x<M
1. Calcular el numero máximo M de hectáreas que poseen los socios.
2. Determinar el porcentaje de fincas con una superficie mayor a 5 Ha.
3. ¿Cuál es la superficie mínima del 15% de las parcelas mas grandes?
4. Suponiendo que todas las parcelas son cuadradas, obtener la función de densidad del perímetro de las parcelas.
5. ¿Qué porcentaje de fincas tiene un perímetro inferior a 800m?
Resolviendo el punto 1. obtengo que M=8 y el punto 2: 0.5844
Gracias y un saludo
Buenas Alfonso:
Tanto el punto 1 como el 2, me da el mismo resultado que a ti.
El punto 3, creo adivinar que es un problema de tipología inversa, es decir, te dan el porcentaje y debes hallar la superficie, en este caso.
Me explico, si tenemos en cuenta la función de distribución acumulada de tú ejercicio:
· F(X): 0 si x ≤ 1
· F(X): (2/77)·(0.5x^2 + x - 3/2) si 1 < x < 8
· F(X): 1 si x ≥ 8
El apartado 3, nos indica una proporción, 15% de las parcelas más grandes. Bien, ¿y cuales son las parcelas más grandes? Pues serían aquellas que estén próximas a 8 Ha, pero si volvemos a repasar nuestra función acumulada, podemos comprobar que da igual que esté próximo a 8 Ha o no, en esa franja la función a usar es la siguiente:
· F(X): (2/77)·(0.5x^2 + x - 3/2) si 1 < x < 8
Por lo tanto, yo establecería la solución de la siguiente manera:
· P(X ≤ x) = 0.15
Donde la función a emplear para las parcelas más grandes es la siguiente:
· P(X ≤ x) = (2/77)·(0.5x^2 + x - 3/2) = 0.15
Obtenemos la solución para la variable x:
· x1 ≈ -4.943349
· x2 ≈ 2.943349
La superficie debe ser positiva, por lo que la solución es x2.
Es decir, la superficie mínima del 15% de las parcelas grandes es de, aproximadamente 2.943349.
Respecto a los apartados 4 y 5, si suponemos que las parcelas son cuadradas (tal y como menciona el apartado 4), la función que se podría usar es la llamada función Uniforme.
Eso sí, tendrías que realizar relaciones entre área y perímetro.
· PD: Te borro aquellos mensajes incompletos.
Un saludo.
hola, necesito ayuda urgente con este ejercicio, mil gracias
El volumen que una maquina de llenado automatico deposita en las latas de una bebida gaseosa tiene una
distribucion normal con media de 34 cl y desviacion estandar de 1,5 cl. Si se desechan aquellas latas que tienen
menos de 33 cl, ¿Cuál es la proporcion de latas desechadas?
Buenas Ivonny Sierra:
Te aconsejo que antes de pedir ayuda respecto a un ejercicio, te mires los que tenemos aquí publicado, te digo esto para no repetir ejercicios ya que eso no ayuda a nadie.
Respecto a tú ejercicio, está resuelto en el siguiente problema: Problema 44. (El primer apartado en concreto es el tú requieres).
Un saludo.
Holas buenas
Tengo una duda con un ejercicio, tengo que hallar la funcion de distribucion
f(x)={(1/25)x 0<x<5,
1/25(10-x) 5<x<10,
0 en otro caso
}
He estado buscando un ejercicio parecido en el blog pero no le encontrado, no se entre que valores se ponen los limites de las integrales
Un saludo, Miguel
Muchas gracias por su ayuda
Buenas Miguel:
Hay varios ejemplos en el blog de como resolver tú problema, por ejemplo el siguiente:
· Problema 31.
Aún así, te lo voy a resolver, es relativamente fácil. Este tipo de ejercicios se resuelve teniendo en cuenta los intervalos de la función de distribución.
Así que trabajamos por partes, por cada intervalo.
· Intervalo: 0 < x < 5:
· F(x) = {Integral entre 0 y x} ʃ(1/25 · t)dt
Como podrás comprobar escribir integrales es complicado por comentarios, además son integrales inmediatas, así que te pongo las soluciones directamente (y para comprobarlo, cómo se obtendrían con el software wxMaxima)
>> integrate((1/25)*t,t,0,x)
Para el primer intervalo (0 < x < 5), tendríamos el siguiente resultado:
· F(x) = (1/50)· x^2
· Intervalo: 5 < x < 10:
· F(x) = {Integral entre 0 y 5} ʃ(1/25 · t)dt + {Interal entre 5 y x} ʃ(1/25 · (10 - t))dt
>> integrate((1/25)*t,t,0,5)+ integrate((1/25)*(10-t),t,5,x);
Para el segundo intervalo (5 < x < 10), tendríamos el siguiente resultado:
· F(x) = -1 + (2/5)·x - (1/50)·x^2
Por lo tanto, como solución, nuestra función de distribución será:
· F(x)= 0,.................. x ≤ 0
· F(x)= (1/50)·x^2,......... 0 < x < 5
· F(x)= -1+(2/5)·x-(1/50)·x^2,..... 5 < x < 10
· F(x)= 1,.................. x ≥ 10
Un saludo.
Buenas, qué tal?
Felicitaciones por el blog, lo acabo de encontrar y me ha salvado!
Me llamo Agustina y necesito una ayuda con un ejercicio, pero no sé si publicarlo, me ayudaría?
Tal vez por e-mail o como guste, si es que gusta :D
Saludos y que ande bien.
Buenas Agustina:
Antes de publicar un ejercicio por comentarios, te recomiendo que revises los ejercicios que tenemos publicados, y en caso de no encontrar ninguno igual, te invito a que lo publiques en el lugar indicado.
Quizás alguien te pueda ayudar o incluso nosotros mismos.
Un saludo y me alegro de que el blog te sirva de ayuda.
Quería darte las gracias por este blog me ha sido de mucha ayuda :) lejos lo mejor que he encontrado en internet.
Hola tengo un ejercicio que no me sale...Gracias
Una lampara se enciende todos los d as a las 7 p.m. Se sabe que su tiempo de duraci on, desde que
se encendi o por primera vez, es una v.a. X exp(1=100) medida en d as. La l ampara se apaga al
otro d a a las 7 a.m. Sea T el tiempo que dura encendida la l ampara, un determinado d a, desde
que se encendi o (a los efectos de T, luego de dicho d a suponemos que la l ampara permanece
apagada).
a) Indicar qu e tipo de variable aleatoria es.
b) Hallar la probabilidad de que la l ampara se queme antes de que sea apagada.
c) Hallar la probabilidad de que la l ampara se queme exactamente cuando se va a apagar, ¿hay
que usar la v.a. T o la v.a. X?.
Publicar un comentario