Ej77. Se lanza un satélite artificial con destino a Marte en un viaje de 100 millones de kilómetros. El número medio de partículas potencialmente peligrosas para el satélite por cada millón de kilómetros de trayectoria es de 3.
Se sabe además que estas partículas se distribuyen al azar y que los números de partículas encontradas en tramos disjuntos de la trayectoria son independientes. Suponemos también que el satélite colisiona con todas las partículas que encuentra en su camino.
La NASA se quejaba de la mala suerte, porque el satélite recibió más de 50 impactos en los primeros 10 millones de kilómetros. ¿Es razonable su queja?
Realizamos una recopilación de datos del enunciado del problema:
· X ≡ 'Nº de colisiones de partículas contra el satélite'.
· La variable aleatoria X sigue una distribución Poisson: X ~ P(3) partículas/(millón km trayectoria).
..3..--- 1
..λ..--- 10
Por lo tanto, el número medio de partículas potencialmente peligrosas por 10 millones de kilómetros de trayectoria:
· λ = (3·10)/1 = 30
Determinaremos, si se puede aproximar a la Normal, para ello, se deben cumplir la siguiente condición:
1. λ > 25 → 30 > 25 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
Por lo tanto: X ~ N(λ, √λ) = N(30, √30).
La probabilidad que debemos obtener, aplicando el factor de corrección, es:
Operamos:
Buscamos el valor en las tablas de la Normal: Φ(3.74) = 0.4999
Y obtenemos la probabilidad requerida:
Por lo tanto, la probabilidad de que el satélite colisione con más de 50 partículas en sus primeros 10 millones de kilómetros de trayectoria es de, aproximadamente 0.0001, en otras palabras, la NASA tiene razón en quejarse de mala suerte ya que la probabilidad de que choque más de 50 partículas es muy baja..

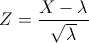
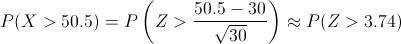




0 comentarios:
Publicar un comentario