Problema71: VAC

Ej71. La longitud de cierta pieza se distribuye con función de densidad:

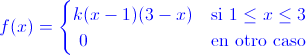
Se consideran válidas las piezas cuya longitud esté comprendida entre 1.7 y 2.4 cm. Se pide:

a) Determinar el valor de k para que f(x) sea una función de densidad legítima.

b) Calcular la probabilidad de que una determinada pieza sea útil.


Apartado a)

Empleamos la expresión de función de densidad de probabilidad:

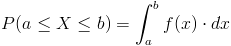
Para los intervalos expuestos en el enunciado del problema, en este caso:

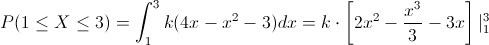
Sustituimos valores:

P(1 ≤ X ≤ 3) = k·[2(3² - 1²) - (1/3)(3³ - 1³) - 3(3 - 1)] = (4/3)·k

Para que una variable aleatoria continua posea una función de densidad de probabilidad, tienen que cumplirse las siguientes condiciones:

1. f(x) > 0,...para todo x.

2.

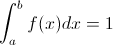
La función f(x) es mayor que cero, para ello, k debe ser mayor que cero, por lo que nos queda, satisfacer la segunda condición:

k = 3/4

Y así, obtenemos el valor de k y la solución de este apartado, para que f(x) sea una función de densidad de probabilidad, el valor de k es de 3/4.

Por lo tanto, la función de densidad de la variable aleatoria continua X queda:

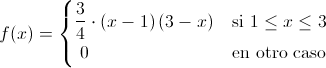
Apartado b)

Para que una pieza sea útil, debe estar comprendida su longitud entre 1 y 3. Empleamos la expresión de función de distribución acumulada para tal fin:

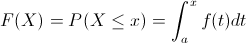
En nuestro caso, el intervalo que tenemos que realizar cálculos es: 1 ≤ x ≤ 3:

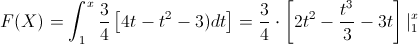
Sustitumimos valores:

F(X) = (3/4)·[2(x² - 1) - (1/3)(x³ - 1) - 3(x - 1)]

Por lo tanto, la función de distribución acumulada queda tal y como se muestra a continuación:

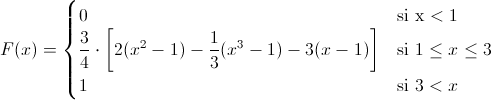
Una vez obtenida la función de distribución acumulada, podemos calcular cualquier probabilidad, en nuestro caso:

P(1.7 ≤ X ≤ 2.4) = F(2.4) - F(1.7)

Sustituimos valores:

(3/4)·[2(2.4²-1)-(1/3)(2.4³-1)-3(2.4-1)]-(3/4)·[2(1.7²-1)-(1/3)(1.7³-1)-3(1.7-1)] =2009/4000

Por lo tanto, la probabilidad de que una determinada pieza sea útil es de 0.50225.