Problema64: VAD

Ej64. Una caja contiene 5 esferas rojas y 10 blancas. Si se seleccionan 8 esferas aleatoriamente y no hay reemplazamiento, determinar la probabilidad de que:

a) 4 sean rojas.

b) Todas sean blancas.

c) Al menos una sea roja.

Realizamos una recopilación de datos del enunciado del problema:

· R ≡ 'Nº esferas rojas'.
· B ≡ 'Nº esferas blancas'.
· La variable aleatoria R y B sigue una distribución Hipergeométrica: X ~ HG de parámetros:
· Número total de unidades: N = 5+10 = 15.
· Para esferas Blancas: Tamaño de la muestra: n = 5.
· Para esferas Rojas: Tamaño de la muestra: n = 10.
· Número total de unidades seleccionadas aleatoriamente: r = 8.

Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.

Apartado a)

Debemos hallar la siguiente probabilidad:

Por lo tanto, la probabilidad de que se obtengan cuatro esferas rojas es de, aproximadamente, 0.163170.

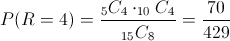
Apartado b)

Debemos hallar la siguiente probabilidad:

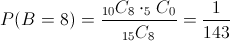
Por lo tanto, la probabilidad de que las ocho esferas sean blancas es de, aproximadamente, 0.006993.

Apartado c)

Debemos hallar la siguiente probabilidad:

P(R ≥ 1) = 1 - P(R < .1) = 1 - P(R = 0)

Para tal fin, emplearemos el software R:

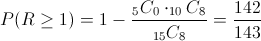
Por lo tanto, la probabilidad de que se obtengan al menos una esfera roja es de, aproximadamente, 0.993007.