En este capítulo se abordará las expresiones matemáticas básicas para el estudio de Cartas de Control.
Se entiende por control estadístico de la calidad mediante cartas de control, el estimar los parámetros de un proceso de producción y así, determinar la idoneidad del mismo.
En este apartado se verán las cartas de control de límite 3-σ. Las cartas de control que se estudiarán, se dividen:
- Cartas de Control de Variables: Las cartas: Ẍ, R.
- Cartas de Control de Atributos: Las cartas: p, C, U.
Análisis de Patrones en Cartas de Control.
Los criterios para discernir si un proceso mediante cartas de control, esté fuera o no de control, serán los descritos y proporcionados por: Western Electric Handbook 1956.
Criterios para que un proceso esté fuera de control:
- Un punto cae más allá de los límites de control 3-σ (Límites de actuación).
- Dos de tres puntos consecutivos, caen más allá de un límite 2-σ (Límites de advertencia).
- Cuatro de cinco puntos consecutivos, están a una distancia 1-σ o mayor de la línea central.
- Ocho puntos consecutivos de la gráfica, están al mismo lado de la línea central.
Carta de Control Ẍ.
Pertenece a la tipo de cartas de control de variables. X ~ N(μ, σ).
- Si: μ y σ son conocidos:
- Si: μ y σ son desconocidos: Tomamos muestras de tamaño n.
Sea R el rango, si E(W) = d2, entonces un estimador insesgado de σ es:
·

Siendo:
·

Por lo tanto, los límites superior e inferior son:
·
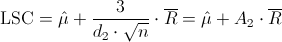
·
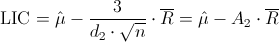
Donde A2 y d2, están tabulados para varios valores de n.
Carta de Control R.
Pertenece a la tipo de cartas de control de variables. X ~ N(μ, σ).
·

Por lo tanto:
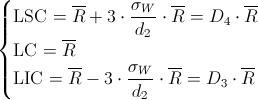
Donde:
·
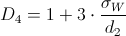
·

Están tabulados para varios valores de n.
Carta de Control p.
Pertenece a la tipo de cartas de control de atributos. Esta carta consiste en la fracción de artículos defectuosos. Sea D, el número de unidades defectuosas en una muestra aleatoria de tamaño n. D ~ B(n, p).
·

·

·

Por lo tanto:
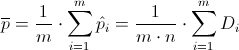
Carta de Control C.
Pertenece a la tipo de cartas de control de atributos. Esta carta consiste en el número de defectos. Sea C, el número de defectos en una muestra aleatoria de tamaño n. C ~ P(λ).
El seguir una distribución de Poisson: E(C) = Var(C) = λ.
·

Por lo tanto:
Carta de Control U.
Pertenece a la tipo de cartas de control de atributos. Esta carta consiste en el número de defectos por unidad. Sea U, el número de defectos por unidad en una muestra aleatoria de tamaño n.
· U = C/n
· E(U) = λ/n.
· Var(U) = λ/n2.
·

Por lo tanto:
Longitud de Desplazamiento Promedio.
Sea Y, el número de puntos en la carta de control hasta que uno cae fuera de los límites k-σ. Y ~ G(p)
El seguir una distribución de geométrica: E(Y) = 1/p = LDP.
Donde:
p = 1 - P(μW - k·σW < . W < . μW + k·σW)
Estimación de la Capacidad del Proceso.
Es el rendimiento del proceso cuando opera bajo control. X ~ N(μ, σ).
El cociente de capacidad del está definido por la expresión:
Siendo:
· 6·σ ≡ Capacidad básica del proceso.
· 3·σ ≡ Tolerancia natural.
Este parámetro se interpreta de la siguiente manera: Sea el % del ancho de las especificaciones utilizadas en el proceso:
Si:
· CCP > 1 ≡ Pocas unidades defectuosas.
· CCP = 1 ≡ Caso normal: 0.27% no cumplen las especificaciones.
· CCP < .1 ≡ Número grande de unidades que no cumplen las especificaciones.
CCP, es la capacidad potencial del proceso, siendo el cociente de capacidad real del proceso:
Si CCP = CCPk, entonces el proceso está centrado en la dimensión nominal.
Una muestra del contenido del fichero que se puede descargar correspondiente a este capítulo, se muestra a continuación:
Se puede descargar los datos tabulados de este tema: Control Estadístico de Calidad: Cartas de Control, anteriormente mostrado, en el siguiente enlace:
 |  | Cartas de Control. |
 |  | Cartas de Control. |
A continuación, se disponen de una colección de problemas resueltos.












11 comentarios:
Buenas!!!
Estoy resolviendo un tipo test sobre este tema y ando un poco liada. Te voy a decir las reguntas a ver si puedes ayudarme.
1. En una carta de control R, el limite inferior se toma como 0 cuando:
a. Es negativo
b. Nunca, puesto que R siempre es positivo.
c. Cuando descubrimos que el proceso esta fuera de control.
2. Uno de los usos de las cartas de cntrol de Sheward es seguir el curso del proceso para:
a. Verificar si cumple las especificaciones
b. Detectar posibles desviaciones de la media de su valor nominal.
c. Mantener el proceso dentro de los limites de tolerancia.
3. Que el cociente de capacidad CCP de un proceso sea menor que 1, significa:
a. Esta fuera de control
b. Esta descentrado
c. No cumple las especificaciones
Ayy perdona por el tochon!! gracias!!!
Buenas A. Bella:
Te recomiendo que repases, al menos, la teoría que en este capítulo se presenta.
Las respuestas son:
· 1. La a, ya que el límite inferior debe ser positivo por definición (es más, dichos datos están tabulados y puedes comprobar que el valor menor es el cero).
· 2. El señor Shewhart (no le cambies el apellido) desarrolló los gráficos para el control de productos industriales con el principal objetivo de investigar si
un proceso se encuentra bajo control estadístico.
¿Y cuál es entonces la respuesta? Pues vamos a analizar cada una de ellas.
· Respecto a la respuesta a: Si cambiamos la palabra verificar por investigar o controlar y asumimos que las especificaciones son las dadas por la propia carta de control, podemos decir que se ésta es la respuesta correta.
· Respecto a la respuesta b: Realmente, la carta de control se fija en el teorema del límite central y su consolidación es que todos los datos obtenidos (para que el proceso esté bajo control) estén o marquen una tendencia en su valor nominal. Ésta podría ser una posible candidata a ser la respuesta correcta pero realmente, tal y como está redactada, está incompleta, ya que el fin de esta técnica es controlar un suceso en sí para poder actuar, no simplemente detectar desviaciones de un parámetro.
· Respecto a la respuesta c: Las cartas de control no se encargan de mantener el proceso en unos límites establecidos, simplemente de mostrarlos y el responsable en la materia tendrá que evaluarlos. En caso de que el proceso esté fuera de control, se deberán tomar medidas. Por lo tanto, descartaría esta respuesta.
Para este enunciado, me quedaría con la respuesta a.
· 3. La c. CCP < 1 ≡ Número grande de unidades que no cumplen las especificaciones.
Un saludo.
Hola!!!
Muchisimas gracias! por las respuestas y por detallarme cada una de ellas. La verdad es que me ha quedado todo super claro.
Estoy resolviendo un test que me caera en el examen de la convocatoria de septiembre (será 80% igual) y me van surgiendo dudillas. Podria preguntarte algunas cosas mas? :) Si no es mucho pedir.
Un saludo
Hola!! Las escribo por si me pudieses ayudar!
1. En un proceso bajo control y centrado:
a. Todos los articulos cumplen las especificaciones
b. El cociente de capacidad es mayor que 1
c. Los cocientes de capacidad CCP y CCPk coinciden
(estoy entre la a y la b, aunque me decanto mas por la b)
2. Se usa una carta de control p̅ cuyo l.i. es 0, en un proceso bajo control. A partir de un cierto momento, los puntos de la carta se situan todos por debajo de la linea central. Que le ocurre a la LMR?
a. Disminuye
b. Disminuye hasta cierto valor a partir del cual comienza a subir.
b. Aumenta
(según lo que he leido, creo que la correcta es la a, pero no estoy segura)
3. En un proceso, los cocientes de capacidad CCP y CCPk siempre verifican:
a. CCPCCPk
4. Un proceso que se está controlando mediante una carta de X̅ experimenta un aumento en la media de magnitud σ/√n . Después de esa salida de control, la posibilidad de que un punto de la carta escape del limite inferior 2-sigma es:
a. Mayor que antes del aumento de la media
b. Menor que antes del aumento de la media
c. No cambia porque el aumento de la media obliga a recalcular los límites de control
Perdona otra vez por el tochon, soy la chica de antes. Salgo como anonimo porque no me deja entrar en mi cuenta desde este ordenador.
Por ultimo, me interesaria mucho contribuir con el blog. Me refiero a donar algo (no mucho pero si algo) porque me está siendo de gran ayuda la verdad. Como podria hacerme una cuenta de paypal? La otra opción que he visto es dar los datos de mi tarjeta pero nose, prefiero hacer mejor una transferencia.
Mil gracias!!! Un saludo
Otra vez..lo siento!
a CCP es menor que CCPk
b CCP es igual a CCPk
c CCP es mayor que CCPk
Buenas:
· Pregunta 1. La respuesta correcta es la c. En la teoría de este capítulo lo puedes comprobar.
· Pregunta 2. No se si estás haciendo un curso de estadística general o de un tema especializado, te lo digo por la terminología que usas. ¿Qué es para ti el LMR y l.i.?
En este tema, no te puedo ayudar ya que está fuera de la temática de este capítulo.
· Pregunta 3. No entiendo muy bien esta pregunta. Lo que te puedo decir son dos cosas:
· Si CCP = CCPk => El proceso está centrado en la dimensión nominal.
· El coeficiente CCPk, describe mejor la habilidad del proceso para producir artículos que cumplan las especificaciones ya que tiene en cuenta el ligero descentrado existente.
Ahora bien, ¿cuál es la respuesta correcta? Pues supongo que lo ideal de un proceso es que ambos parámetros coincidan, pero esto no suele pasar, por lo que el parámetro CCP será algo mayor que el CCPk ya que éste segundo, tiene en cuenta otros factores que hacen a la medida más precisa.
· Pregunta 4. Si se aumenta las especificaciones del producto, en este caso la media, la posibilidad de encontrar un punto fuera de los límites de control es mayor. Puedes encontrar problemas resueltos en este capítulo donde puedes comprobarlo (generalmente están relacionados con el parámetro LDP)
Te agradezco tu interés por contribuir con este blog, la manera de hacerlo es mediante PayPal (sistema totalmente fiable que además se emplea en sitios como ebay). Te registras y puedes asociar o una cuenta bancaria o una tarjeta, para más seguridad, puedes asociar una tarjeta virtual (tiene caducidad y un límite de dinero).
Para obtener tu tarjeta virtual, debes preguntarlo en tu oficina bancaria (suelen ser totalmente gratuitas).
La otra forma de contribuir es tal y como lo estás haciendo, comentando dudas (preferiblemente de los problemas que están expuestos en este blog).
Un saludo.
Buenas! Mil gracias de nuevo!
Estoy haciendo un master (rama de ingenieria), bueno terminandolo y la ultima asignatura que me queda es la de ampliación de estadistica y optimización.
LMR es la longitud media de racha, es que en mi tema de cartas de control y capacidad del proceso se habla de ella tambien. Con l.i me referia a limite inferior
Respecto a la pregunta 3, asi es como plantea la pregunta mi profesor en el test aunque lo copie corriendo en la ultima convocatoria e igual me he saltado algo :S
Si me vuelve a caer la pregunta 3 en el examen de septiembre igual me decanto por la respuesta c, o quizas mejor la deje en blanco. Ya veré porque resta puntos.
Con respecto a Paypal, ire a mi banco en cuanto vaya a Espana el proximo mes. No vivo alli y es imposible encontrar aqui un profesor de estadistica que pueda explicarmelo todo en mi idioma. La verdad es que este blog me está ayudando muchisimo! Porque al menos este tema es muy parecido y he visto que el de fiabilidad tambien.
En breve voy a sugerir algunos problemas de examenes. Saludos
Buenas! Propongo un problema.
Un proceso centrado cuya característica de calidad se distribuye normalmente con media µ=100 y desviación típica σ=2, tiene un cociente de capacidad CCP=1,5. Si la media se desvía un 5% de su valor inicial, calcule el cociente CCPk. Cual será el porcentaje de artículos que no cumplen las especificaciones? Explique por qué no es necesario indicar si la desviación es por exceso o por defecto.
Gracias!!!
A mi tambien me interesaria ese problema!! gracias!
Cuando regreses de vacaciones o cuando tengas tiempo. Podrías ayudarme con este problema? Este y el anterior han caído dos veces en exámenes pero me surgen muchas dudas al resolverlos.
En un proceso productivo cuyos artículos pueden clasificarse como defectuosos, el estadístico D=n° de defectuosos en una muestra de tamaño n, tiene distribución binomial de parámetros n y p donde p es la fracción de defectuosos del proceso. Dado que esta distribución no es simétrica (excepto si p=0.5), la probabilidad de que un punto de una carta de control de defectuosos (carta p ̅) esté entre la línea central y el límite superior 3-sigma, no es la misma que la probabilidad de que este entre la línea central y el límite inferior 3-sigma. Sin n=1 y p=0.1
Calcule ambas probabilidades suponiendo el proceso bajo control
Cuál es la probabilidad de una falsa alarma?
Lo mismo si l fracción de defectuosos del proceso pasa a valer 0.15, cual es ahora la LMR (LDP)?
Gracias!
Buenas!
Mi examen es la proxima semana. Podriais ayudarme con los dos problemas anteriores? Gracias.
Un saludo
A. Bella
Publicar un comentario