Este capítulo pretende abordar de forma breve y panorámica, los conceptos necesarios y suficientes relacionados con la Transformada y Antitransformada de Laplace.
Y las dos primeras preguntas que nos pueden surgir es: ¿Para qué es necesario este capítulo? y ¿qué de interés tiene el estudio de esta técnica?. La respuesta a ambas preguntas es bien sencilla, la Transformada de Laplace constituye una parte fundamental de las matemáticas requerida por los ingenieros, matemáticos, físicos y demás ciencias.
Esto es así ya que, la Transformada de Laplace no es más que una herramienta muy útil e incluso se podría denominar imprescindible, para ciertos problemas que presentan difícil solución. Por ejemplo, el empleo de esta herramienta para solucionar Ecuaciones Diferenciales es de gran ayuda, ya que nos disminuye la dificultad de forma considerable ante su resolución por métodos convencionales.
Una definición formal es: Sea f(x) una función en [0, ∞), la Transformada de Laplace de f(x) es la función F(s) definida por la integral:
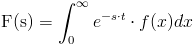
El dominio de F(s) consta de todos los valores de s para los cuales la integral anterior exista.
Y como este capítulo no pretende abordar de forma exhaustiva dicho método, emplearemos la Transformada de Laplace como una herramienta para la resolución de ciertos problemas de cálculo o modelaje, y es por ello, que la premisa fundamental que seguiremos es la de aplicar esta herramienta de forma rápida, fácil y concisa.
Para tal fin, se propone para su uso, una tabla de Transformadas de Laplace que se pueden aplicar de forma directa:
1. Linealidad. Sea c1 y c2 no dependientes de la variable x:
2. Traslación.
3. Cambio de Escala.
4. Potencia de la variable dependiente.
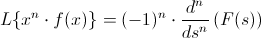
5. Transformada de la Derivada Primera.
De forma genérica:
6. Transformada de la Integral.
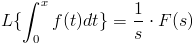
Quizás las propiedades expuestas anteriormente sean las más generales e importantes, éstas, nos servirán de ayuda y soporte para obtener la Transformada de Laplace de una función de otra manera.
Ahora, nos centramos en recorrer el camino contrario, es decir, la Transformada Inversa de Laplace, una definición a esta herramienta: la Transformada inversa de Laplace de F(s) es aquella función única f(t) que es continua en [0, ∞) y satisface:
La función f se denota con el operador inverso de Laplace, L-1{F}. La propiedad de Linealidad está presente en esta herramienta también.
La técnica más simple para identificar las Transformadas inversas de Laplace consiste en reconocerlas mediante tablas cómo la expuesta en este capítulo. En caso de que F(s) no está en una forma reconocible, entonces se podrá transformar, ocasionalmente, en tal forma mediante manipulación algebraica.
Como sugerencia, la forma de proceder generalmente es convertir primero el denominador a una forma que aparezca en las tablas, y posteriormente, trabajar con el numerador.
Para la manipulación del denominador, se expondrán un par de técnicas que nos serán bastantes útiles a la hora de enfrentarnos a cualquier problema de esta índole.
● Completar Cuadrados.
Si tenemos un denominador que presenta la siguiente estructura:
Podemos completar cuadrados si la agrupamos de la siguiente forma:
Siendo:
·
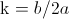
·
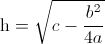
● Fracciones Parciales.
Si tenemos un denominador que presenta la siguiente estructura:
Debemos expresar la función de la siguiente forma:
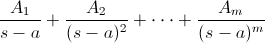
En cambio, si tenemos un denominador que presenta la siguiente estructura:
Debemos expresar la función de la siguiente forma:
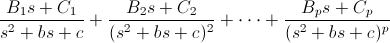
Intentaremos abordar la mayoría de los casos más comunes en los ejercicios expuestos en este capítulo.
Se puede descargar la tabla: Transformada de Laplace, anteriormente mostrada, en el siguiente enlace:
 |  | Transformada de Laplace. |
 |  | Transformada de Laplace. |
Dicha tabla estará en continua revisión y actualización.
Y para concluir, recalcar nuevamente, que la forma de tratar esta herramienta será especialmente, por medio de la tabla expuesta, esto es así ya que la intención principal es de este capítulo es el empleo de la Transformada de Laplace y su uso, no su obtención matemática cuando las funciones a modelar son medianamente complejas.
Ya que para ello, hoy en día se dispone de herramientas potentes y bastante útiles para tales menesteres y sobre todo, porque el meternos de lleno en resolver ciertas integrales de funciones complejas desvirtuarían el propósito de este capítulo, que es el del manejo, uso y aplicación de la herramienta.
Aún así, se exponen de forma casi esquemática, cómo obtener la la Transformada de Laplace mediante el software Maxima y la calculadora Casio ClassPad 330:
| Software: Transformada de Laplace | |
| Maxima | Transformada y Antitransformada de Laplace. |
| Casio ClassPad 330 | Transformada y Antitransformada de Laplace. |
| Transformada de Laplace | ||
| Ejercicios Básicos. | ||
| Problema 1 | Problema 3 | Problema 5 |
| Problema 2 | Problema 4 | Problema 6 |
| Ejercicios: Tablas & Propiedades. | ||
| Problema 1 | Problema 6 | Problema 11 |
| Problema 2 | Problema 7 | |
| Problema 3 | Problema 8 | |
| Problema 4 | Problema 9 | |
| Problema 5 | Problema 10 | |
| Transformada Inversa de Laplace | ||
| Problema 1 | Problema 6 | |
| Problema 2 | Problema 7 | |
| Problema 3 | Problema 8 | |
| Problema 4 | Problema 9 | |
| Problema 5 | Problema 10 | |
| Laplace: Ecuaciones Diferenciales | ||
| Problema 1 | Problema 6 | Problema 11 |
| Problema 2 | Problema 7 | Problema 12 |
| Problema 3 | Problema 8 | |
| Problema 4 | Problema 9 | |
| Problema 5 | Problema 10 | |
NOTA: Las expresiones expuestas no se demostrarán por no entrar en la temática de este capítulo, aún así, es fácil su desarrollo y demostración.





1 comentarios:
Desde la primaria que en matematica me ha ido mas o menos bien y ahora sigo teniendo buenas notas en esta materia. En general en el resto no, pero en las materias practicas me va bastante bien. Por eso muchas veces me pongo a practicar ecuaciones
Publicar un comentario