Variables Aleatorias Discretas y Distribuciones de Probabilidad.

Definiciones Importantes:

Variable Aleatoria: Es una variable que toma valores numéricos determinados por el resultado de un experimento aleatorio.

Es importante distinguir entre variable aleatoria y los posibles valores que ésta puede tomar, se empleará letras mayúsculas, tales como X, para designar la variable aleatoria y correspondiente minúscula, x, para designar un valor posible.

Una variable aleatoria es discreta si sólo puede tomar una cantidad numerable de valores, en cambio, una variable aleatoria es continua si puede tomar todos los valores de un intervalo, este tipo de variables, no se les puede asignar probabilidades a cada valor concreto.

Función de Probabilidad: Denominada como P_x(x), de una variable aleatoria discreta X representa la probabilidad de que X tome el valor x, como función de x. Es decir:

P_x(x) = P(X = x)

Donde la función se evalúa en todos los posibles valores de x.

Sus propiedades se definen como: Sea X una una variable aleatoria discreta con función de probabilidad P_x(x). Entonces:

1. P_x(x) ≥ 0, para cada valor x.

2. Las probabilidades individuales suman 1, es decir:

ΣP_x(x) = 1

Donde la notación indica la suma sobre todos los posibles valores de x.

Función de Probabilidad Acumulada: Denominada como F_x(x₀), de una variable aleatoria discreta X representa la probabilidad de que X no tome un valor superior a x₀, como función de x₀. Es decir:

F_x(x₀) = P(X ≤ x₀)

Donde la función se evalúa en todos los posibles valores de x₀.

Sus propiedades se definen como: Sea X una una variable aleatoria discreta con función de probabilidad acumulada F_x(x₀). Entonces:

1. 0 ≤ F_x(x₀) ≤ 0, para cada valor x₀.

2. Si x₀ y x₁ son dos números tales que x₀.x₁, entonces:

F_x(x₀) ≤ F_x(x₁)

Relación entre Función de Probabilidad y Función de Probabilidad Acumulada: Sea X una variable aleatoria discreta con función de probabilidad P_x(x) y función de probabilidad acumulada F_x(x₀). Entonces:

F(x) = ΣP_x(x) = 1

Donde la notación indica que la suma es sobre todos los posibles valores de x que son menores o iguales que x₀.

Valor Esperado.

Denominado como E(X), de una variable aleatoria X se define como:

E(X) = Σx·P_x(x)

Donde la notación indica que la suma es sobre todos los posibles valores de x.

El valor esperado de una variable aleatoria se conoce como su media y se representa μ_x.

Sea X una variable aleatoria discreta con función de probabilidad P_x(x), y sea g(X) una función de X. Entonces, el valor esperado, E(g(X)), de esta función se define como:

E[g(X)] = Σg(x)·P_x(x)

Varianza.

Sea X una variable aleatoria discreta. Se denomina la varianza, σ_x, y se obtiene como:

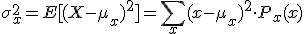
Otra forma alternativa de expresar la varianza es de la siguiente manera:

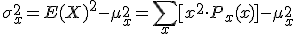
La desviación típica, σ_x, es la raíz cuadrada positiva de la varianza.

Función de Probabilidad Conjunta.

Sean X e Y dos variables aleatorias discretas. La función de probabilidad conjunta representa la probabilidad de que simultáneamente X tome el valor x e Y tome el valor y, como función de x e y. Se usa la notación P_X,Y(x, y), de donde:

P_X,Y(x, y) = P(X = x ∩ Y = y)

Propiedades:

1. P_X,Y(x, y) ≥ 0, para cualquier par de valores x e y.

2. La suma de las probabilidades conjuntas P_X,Y(x, y) sobre todos los posibles pares de valores debe ser 1.

Función de Probabilidad Marginal.

Sean X e Y dos variables conjuntamente distribuidas. En este contexto, la función de probabilidad de la variable aleatoria X se denomina función de probabilidad marginal, y se obtiene sumando las probabilidades conjuntas sobre todos los posibles valores de Y, es decir:

P_X(x) = ΣP_X,Y(x, y)

Análogamente, la función de probabilidad marginal de la variable aleatoria Y es:

P_Y(y) = ΣP_X,Y(x, y)

Función de Probabilidad Condicional.

Sean X e Y dos variables conjuntamente distribuidas. La función de probabilidad condicional de la variable aleatoria Y, dado que la variable aleatoria X toma el valor x, representa la probabilidad de que Y tome el valor y, cuando se especifica el valor x para X.

Esta función, se representa como P_Y|X(y|x), y por la condición de probabilidad condicional:

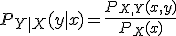
Variables Aleatorias Independientes.

Las variables aleatorias X e Y son independientes si y sólo si su función de probabilidad conjunta es el producto de sus funciones de probabilidad marginal, es decir, si y sólo si:

P_{x, y}(x, y) = P_x(x)·P_y(y)

Para todos los posibles valores x e y.

Función de Probabilidad Conjunta Acumulada.

Se denomina como F_X,Y(x₀, y₀), de un par de variables aleatorias discretas X e Y representa la probabilidad de que simultáneamente X no exceda del valor x₀ e Y no supere el valor y₀, como función de x₀ e y₀. Es decir:

F_X,Y(x₀, y₀) = P(X ≤ x₀ ∩ Y ≤ y₀)

Donde la función se evalúa en todos los valores de x₀ e y₀. Esto puede escribirse:

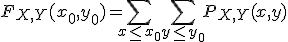
Donde la notación indica que la suma es sobre todos los pares de valores x e y que las variables aleatorias pueden tomar simultáneamente, y que satisfacen x ≤ x₀ e y ≤ y_0.

Esperanza con Función de Probabilidad Conjunta.

Sean X e Y dos variables discretas aleatorias con función de probabilidad conjunta P_{x, y}(x, y). La esperanza de una función g(X, Y) de estas variables aleatorias se define como:

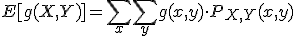
Covarianza.

Sean X una variable aleatoria con media μ_X, y sea Y una variable aleatoria con media μ_Y. La covarianza es:

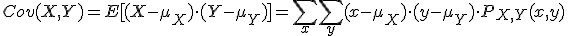
Una expresión alternativa es:

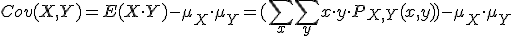
Hay que tener en cuenta que, si un par de variables aleatorias son estadísticamente independientes, la covarianza entre ellas es igual a cero. Sin embargo, que la covarianza valga cero, no implica, a priori, que el par de variables sea independientes.

Distribución Binomial.

Supongamos que un experimento aleatorio tiene sólo dos resultados posibles mutuamente excluyentes y conjuntamente exhaustivos, “éxito” y “fracaso”, y que p es la probabilidad de obtener éxito en cada repetición.

Si se realizan n repeticiones independientes, la distribución del número de éxitos, X, resultante se denomina distribución binomial. Su función de probabilidad es:

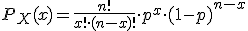
para x = 0, 1, 2, ..., n.

Media de la distribución binomail: μ_x = E(X) =n·p

Varianza de la distribución binomial: σ_x² = E[(X - μ_x)² = n·p·(1 - p)

Distribución Geométrica.

Es una serie de ensayos de Bernoulli independientes, con probabilidad constante p de un éxito, sea que la variable aleatoria X denote el número de ensayos hasta el primer éxito.

Entonces X tiene una distribución geométrica con parámetro p.

P(X = x) = p·(1 - p)^x-1

Donde x = 1, 2, 3, ...

Su media: μ_x = E(X) = 1/p

Su varianza: σ_x² = V(X) = (1 - p)/p²

Distribución Binomial Negativa.

Surge de un contexto semejante al que conduce a la distribución geométrica. La distribución que asigna a la variable Y, el número de ensayo en el que ocurre el r-ésimo éxito.

Su función de probabilidad es:

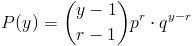
para y = r, r + 1, r + 2, ....

Media de la distribución binomail negativa: μ_x = E(X) =r/p

Varianza de la distribución binomial negativa: σ_x² = E[(X - μ_x)² = r·(1 - p)/p²

Distribución Hipergeométrica.

Supongamos que se elige una muestra aleatoria de tamaño n de un conjunto de N elementos, S de los cuales son éxitos.

La distribución del número de éxitos, X, en la muestra se denomina distribución hipergeométrica. Su función de probabilidad es:

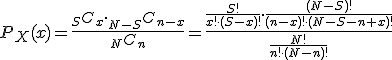
donde x puede tomar valores enteros entre el máximo de 0 y [n – (N – S)] y el mínimo de n y S.

Su media: μ_x = E(X) =n·p

Su varianza:

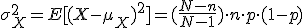
Si el tamaño muestral n es muy pequeño en relación al número total de elementos, N, las probabilidades hipergeométricas son muy parecidas a las binomiales, y se puede usar la distribución binomial en vez de la hipergeométrica.

Distribución De Poisson.

Se dice que la variable aleatoria X sigue una distribución de Poisson si tiene la función de probabilidad:

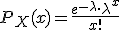
para x = 0, 1, 2, ...

Donde λ es cualquier número tal que λ > 0.

La media: μ_x = E(X) = λ

La varianza: σ_x² = E[(X - μ_x)² = λ

Aproximación a Poisson de la Distribución Binomial.

Sea X el número de éxitos resultantes de n ensayos independientes, cada uno con probabilidad de éxito p.

La distribución del número de éxitos X es binomial con media n·p. Sin embargo, si el número de ensayos n es grande y n·p tiene un tamaño moderado (preferiblemente n·p ≤ 7), esta distribución puede aproximarse bien por la distribución de Poisson de media λ = n·p.

La función de distribución aproximada es:

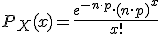
Para x = 0, 1, 2, ...

---

A continuación, se disponen de una colección de problemas resueltos.

Problemas: Variables Aleatorias Discretas.
Problema 1	Problema 11	Problema 21	Problema 31	Problema 41	Problema 51	Problema 61	Problema 71	Problema 81
Problema 2	Problema 12	Problema 22	Problema 32	Problema 42	Problema 52	Problema 62	Problema 72	Problema 82
Problema 3	Problema 13	Problema 23	Problema 33	Problema 43	Problema 53	Problema 63	Problema 73	Problema 83
Problema 4	Problema 14	Problema 24	Problema 34	Problema 44	Problema 54	Problema 64	Problema 74	Problema 84
Problema 5	Problema 15	Problema 25	Problema 35	Problema 45	Problema 55	Problema 65	Problema 75	Problema 85
Problema 6	Problema 16	Problema 26	Problema 36	Problema 46	Problema 56	Problema 66	Problema 76	Problema 86
Problema 7	Problema 17	Problema 27	Problema 37	Problema 47	Problema 57	Problema 67	Problema 77	Problema 87
Problema 8	Problema 18	Problema 28	Problema 38	Problema 48	Problema 58	Problema 68	Problema 78	Problema 88
Problema 9	Problema 19	Problema 29	Problema 39	Problema 49	Problema 59	Problema 69	Problema 79	Problema 89
Problema 10	Problema 20	Problema 30	Problema 40	Problema 50	Problema 60	Problema 70	Problema 80	Problema 90