Teoría Elemental de la Probabilidad.

Si nos basamos simplemente en la información muestral, es imposible determinar exactamente la reacción de la totalidad de la población, cualquier medida de dicha reacción, inevitablemente, llevará consigo una cierta incertidumbre.

Aunque no es posible, basándose en la muestra, deducir cierta información sobre la población, puede ser posible hacer afirmaciones precisas sobre la naturaleza de la incertidumbre.

Estas afirmaciones se expresan en el lenguaje de la probabilidad.

Para realizar un estudio sistemático de probabilidad se necesita una cierta terminología.

Definiciones importantes.

Un experimento constituye un proceso con un resultado que no se puede predecir ciertamente con anterioridad.

Se llama espacio muestral al conjunto de todos los posibles resultados de un experimento. Se le suele denotar con la letra griega Ω.

Por ejemplo, el típico ejemplo de lanzar una moneda. Se identifica el experimento el hecho de lanzar una moneda.

Y el espacio muestral sería si sale cara o cruz.

Por lo tanto, el espacio muestral de dicho experimento sería:

Ω = {“cara”, “cruz”}

Otro típico ejemplo sería el de un dado. El experimento se identifica con tirar un dado no trucado, y el espacio muestral sería los posibles valores que obtendríamos al lanzar el dado.

Ω = {1, 2, 3, 4, 5, 6}

En este caso, los seis posibles valores que posee un dado.

Otra definición importante a tener en cuenta es la denominada evento o suceso.

Un evento o suceso, es un subconjunto de un espacio muestral.

Por ejemplo en el ejemplo anterior del dado, el espacio muestral será los posibles valores de salida al lanzar el dado, definido por:

Ω = {1, 2, 3, 4, 5, 6}

Ahora bien, lo que se requiere es estudiar la probabilidad de que al lanzar el dado, su resultado sea par, por lo tanto, el evento o suceso, será:

A Ξ “Al lanzar el dado sea par”

Por lo tanto, el suceso es:

A = {2, 4, 6}

Se podría también, definir el suceso de que al lanzar el dado, el resultado sea impar.

Se debe definir de la siguiente manera:

B Ξ “Al lanzar el dado sea impar”

Por lo tanto, el suceso es:

B = {1, 3, 5}

Combinación de Sucesos.

Con frecuencia, se constituyen sucesos mediante la combinación de sucesos más sencillos.

La unión de dos sucesos A y B, se denota por:

AUB

Es el conjunto de resultados que pertenecen ya sea a A o B, o a ambos. Por lo tanto, la unión se debe interpretar como “A o B”.

La intersección de dos eventos A y B se denota por

A∩B

Es decir, constituye el conjunto de resultados que pertenecen tanto a A como a B. Por lo tanto, la intersección debe interpretarse como “A y B”.

El complemento de un evento E se denota por

Ē

Es el conjunto de resultados que no pertenecen a E. Por lo tanto, debe interpretarse como “no E”. Analíticamente y en términos de probabilidad, se expresa como:

P(Ē) = 1 - P(E)

Sucesos Mutuamente Excluyentes.

Existen ciertos sucesos que nunca se presentan simultáneamente. Por ejemplo, es imposible que una moneda que se arroje al aire caiga a la vez en cruz y en cara, a estos sucesos se le llama mutuamente excluyentes.

Se dice que los sucesos A y B son mutuamente excluyentes si no tienen resultados en común.

Por ejemplo, sean los sucesos:

A Ξ “Lanzar un dado” y B Ξ “Llueva en Jerez de la Frontera”

Estos dos sucesos, no tienen resultados en común, por lo tanto se le denomina sucesos mutuamente excluyentes.

A la terminología de mutuamente excluyentes, también se le suele llamar disjuntos.

Su definición: Sean A y B dos sucesos mutuamente excluyentes. Entonces la probabilidad de la unión es la suma de las probabilidades individuales de los sucesos, es decir:

P(AUB) = P(A) + P(B)

De manera más general, si E₁, E₂, ..., E_n son sucesos mutuamente excluyentes, entonces:

P(E₁ ∪ E₂ ∪···∪ E₃) = P(E₁) + P(E₂) +···+ P(E_n)

Probabilidades.

Todo suceso dentro de un espacio muestral tiene una probabilidad de ocurrir.

Con frecuencia, se representa la probabilidad con la letra P.

Dado un experimento y cualquier evento A:

• La expresión P(A) denota la probabilidad de que ocurra el suceso A.
• P(A) constituye la proporción de veces que se representa el evento A en el tiempo, si es que el experimento se realiza una y otra vez.

Axiomas de la Probabilidad.

1. Sea un espacio muestral Ω, entonces: P(Ω) = 1.
2. Para cualquier suceso A, 0 ≤ P(A) ≤ 1.
3. Sea A un suceso en el espacio muestral Ω, y sean Oi los resultados que componen el suceso A, entonces: .

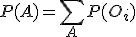El primer axioma establece que el resultado de un experimento siempre está en el espacio muestral. Esto es obvio, ya que por definición, el espacio muestral contiene todos los valores posibles del experimento.

El segundo axioma, dice que la frecuencia alargo plazo de cualquier suceso siempre se encuentra entre 0 y 100%, es decir, entre 0 y 1.

El tercer axioma, quiere decir que la probabilidad de cualquier suceso, es la suma de los elementos que lo componen.

Espacios Muestrales Con Resultados Igualmente Probables.

En algunos experimentos se puede construir un espacio muestral en el cual todos los resultados sean igualmente probables.

Un ejemplo sencillo es el lanzar un dado, en el cual, el espacio muestral es:

Ω = {1, 2, 3, 4, 5, 6}

y cada uno de los resultados tiene una probabilidad de 1/6, teniendo en cuenta que el dado no esté trucado.

Otro tipo de experimentos que tiene resultados igualmente probables es la selección aleatoria de un elemento a partir de una población de elementos.

Por lo tanto, una población a partir de la cual se muestrea un elemento en forma aleatoria constituye un espacio muestral con resultados igualmente probables.

Si Ω, es un espacio muestral que contiene a N elementos igualmente probables, y si A es un suceso que contiene k resultados, entonces se deduce que la probabilidad del suceso A es:

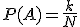
Regla de la Suma.

Sea A y B cualquier suceso, entonces:

P(AUB) = P(A) + P(B) - P(A∩B)

En caso que los sucesos A y B sean mutuamente excluyentes, la suma será:

P(AUB) = P(A) + P(B)

Ordenación y Conteo de Resultados.

Una dificultado práctica que aparece a veces al calcular la probabilidad de un suceso, es la de contar el número de resultados en el espacio muestral y en el suceso en interés.

Para algunos problemas, el uso de permutaciones y combinaciones puede ser útil.

El número de posibles ordenaciones de x objetos es:

x·(x-1)(x-2)···(2)(1) = x!

Permutaciones.

Una permutación constituye un ordenamiento de un conjunto de elementos.

El número de permutaciones, _nP_x ,de n objetos elegidos de un grupo de x en x es el número de posibles ordenaciones cuando x objetos han de ser seleccionados de un total de n y dispuestos en orden:

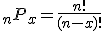
Combinaciones.

A cada grupo distinto de elementos que se puede seleccionar, sin importar el orden, se le llama combinaciones.

Por lo tanto, el número de combinaciones, _nC_x, de n objetos tomados de x en x, es el número de posibles elecciones que pueden ser hechas. Se calcula de la siguiente manera:

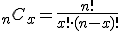
Probabilidad Condicional.

Una probabilidad que se basa en una parte de un espacio muestral se denomina probabilidad condicional.

Sean A y B sucesos con P(B) > 0. La probabilidad condicional de A dado B es:

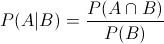
Regla del Producto de Probabilidades.

Sean A y B dos sucesos. La probabilidad de la intersección es:

P(A∩B) = P(A|B)·P(B)

Análogamente:

P(B∩A) = P(B|A)·P(A)

Sucesos Independientes.

Algunas veces, el conocimiento de que un suceso ha ocurrido no cambia la probabilidad de que ocurra otro, en este caso, se dice que los sucesos son independientes.

Dos sucesos A y B son independientes si la probabilidad de cada uno es la misma si ocurren o no los demás sucesos, entonces, se dice que estos sucesos son independientes sí y sólo si:

P(A∩B) = P(A)·P(B)

Si P(A) > 0 y P(B) > 0, entonces A y B son independientes si:

P(A|B) = P(A)

La Regla de la Multiplicación.

Si A y B son dos sucesos con P(B) > 0, entonces:

P(A∩B) = P(B)·P(A|B)

Cuando dos sucesos son independientes, entonces P(A|B) = P(A) y P(A|B) = P(B), así, la regla de la multiplicación se simplifica.

· Si A y B son sucesos independientes, entonces:

P(A∩B) = P(A)·P(B)

En la mayoría de los casos, la mejor manera de determinar si dos sucesos son independientes es comprendiendo el proceso que los produce. He aquí algunos ejemplos:

• Se tira dos veces un dado, es razonable creer, que el resultado de la segunda tirada no se vea afectado por el resultado de la primera. Por tanto, conocer el resultado de la primera tirada no ayuda a predecir el resultado de la segunda tirada. Las dos tiradas son independientes.

• Cierta reacción química se realiza dos veces, utilizando equipos diferentes cada vez. Es razonable creer que el producto de una reacción no afectará la producción de la otra. En este caso los sucesos son independientes.

• Los elementos de una muestra aleatoria se pueden tratar como independientes a menos que la población sea finita y la muestra consista de más de 5% de la población.

Ley de la Probabilidad Total.

Si A₁, ..., A_n, son mutuamente excluyentes y exhaustivos y B es cualquier suceso, entonces:

P(B) = P(A₁∩B) +···+ P(A_n∩B)

De manera equivalente, si P(A_i) > 0 para cada A_i,

P(B) = P(B|A₁)·P(A₁) +···+ P(B|A_n)·P(A_n)

Regla de Bayes.

Caso Especial: Sean A y B sucesos con P(A) > 0, P(Ā) > 0 y P(B) > 0. Entonces:

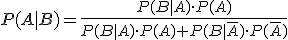
Caso General: Sean A1, ..., A_n sucesos mutuamente excluyentes y exhaustivos con P(A_i) > 0 para cada A_i. Sea B cualquier suceso con P(B) > 0. Entonces:

---

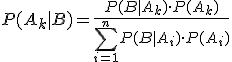
Problemas:

Teoría: Cuestionario Tipo Test.
Problema 1	Problema 11	Problema 21	Problema 31	Problema 41	Problema 51	Problema 61	Problema 71	Problema 81	Problema 91
Problema 2	Problema 12	Problema 22	Problema 32	Problema 42	Problema 52	Problema 62	Problema 72	Problema 82	Problema 92
Problema 3	Problema 13	Problema 23	Problema 33	Problema 43	Problema 53	Problema 63	Problema 73	Problema 83	Problema 93
Problema 4	Problema 14	Problema 24	Problema 34	Problema 44	Problema 54	Problema 64	Problema 74	Problema 84	Problema 94
Problema 5	Problema 15	Problema 25	Problema 35	Problema 45	Problema 55	Problema 65	Problema 75	Problema 85	Problema 95
Problema 6	Problema 16	Problema 26	Problema 36	Problema 46	Problema 56	Problema 66	Problema 76	Problema 86	Problema 96
Problema 7	Problema 17	Problema 27	Problema 37	Problema 47	Problema 57	Problema 67	Problema 77	Problema 87	Problema 97
Problema 8	Problema 18	Problema 28	Problema 38	Problema 48	Problema 58	Problema 68	Problema 78	Problema 88	Problema 98
Problema 9	Problema 19	Problema 29	Problema 39	Problema 49	Problema 59	Problema 69	Problema 79	Problema 89	Problema 99
Problema 10	Problema 20	Problema 30	Problema 40	Problema 50	Problema 60	Problema 70	Problema 80	Problema 90	Problema 100